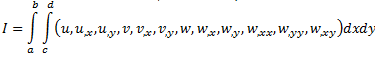ronaldinho52 said:
Dear all,
I am stuck with the problem which is given below;
In this problem the equilibrium equations of the given functional must be derived in u, v, and w directions from which the boundary terms must be found. I think that i have derived the equilibrium equations( 5 equations), but i don't know how to proceed. Does anyone maybe know how to do it??
I think you're missing a name for the integrand. I will use L.
To determine \delta I, integrate L(u + h, \dots, v + k, \dots, w + l, \dots) - L(u, \dots, v, \dots, w, \dots) term by term. You can swap the order of integration so that terms involving derivatives with respect to x are integrated with respect to x first, and terms involving derivatives with respect to y are integrated with respect to y first.
For example, for the u_{,x} term you get:
<br />
\int_a^b \int_c^d h_{,x} \frac{\partial L}{\partial u_{,x}}\,\mathrm{d}x \,\mathrm{d}y<br />
= \int_a^b \left[ h \frac{\partial L}{\partial u_{,x}}\right]_c^d\,\mathrm{d}y - \int_a^b \int_c^d h \frac{\partial}{\partial x} \left(\frac{\partial L}{\partial u_{,x}}\right)\,\mathrm{d}x\,\mathrm{d}y
(The antiderivative with respect to x of h_{,x} is h + A(y) for an arbitrary function A; but it will be the same function at both x = c and x = d, so it cancels out.)
Ideally the conditions of your problem are such that the perturbation h vanishes everywhere on the boundary, so the boundary term vanishes.
With the second derivatives of w you have to integrate by parts twice:
<br />
\int_a^b \int_c^d l_{,xx} \frac{\partial L}{\partial w_{,xx}}\,\mathrm{d}x \,\mathrm{d}y<br />
= \int_a^b \left[ l_{,x} \frac{\partial L}{\partial w_{,xx}} \right]_c^d\,\mathrm{d}y<br />
- \int_a^b \int_c^d l_{,x} \frac{\partial}{\partial x}\left(\frac{\partial L}{\partial w_{,xx}}\right)\,\mathrm{d}x \,\mathrm{d}y<br />
Again, one would hope that the conditions of your problem require that l_{,x} vanishes on the boundary, so the boundary term vanishes. The remaining term is dealt with as for the other first derivatives.
Incidentally, I believe there should be three equilibrium equations (one each for u, v and w) so if you have five then you have made an error somewhere.