Calculus airplane related rates problem ( cosine rule)

[jaychay]

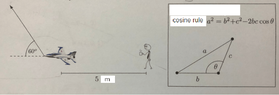
A student has test his airplane and he is far from the airplane for 5 meter.He start to test his airplane by letting his airplane to move 60 degree from the horizontal plane with constant velocity for 120 meter per minute.Find the rate of distance between the student and the plane when the plane is moving 60 degree from the horizontal plane for 10 meter in the air ?

Please help me
I have tried to solve the answer many times but I cannot do it
Thank you in advice

 

[skeeter]

Are you translating this to English from another language? I assume the problem wants to know the rate of change of the distance between the plane and student w/respect to time.

note 120 meters/min = 2 meters/sec

let $r$ be the distance between the student and the airplane at any time $t$ in seconds

$r^2 = (2t)^2 + 5^2 - 2(2t)(5)\cos(120^\circ)$

take the derivative of the above equation w/respect to time, then determine the value of $\dfrac{dr}{dt}$ in meters/sec

 

[jaychay]

Are you translating this to English from another language? I assume the problem wants to know the rate of change of the distance between the plane and student w/respect to time.

note 120 meters/min = 2 meters/sec

let $r$ be the distance between the student and the airplane at any time $t$ in seconds

$r^2 = (2t)^2 + 5^2 - 2(2t)(5)\cos(120^\circ)$

take the derivative of the above equation w/respect to time, then determine the value of $\dfrac{dr}{dt}$ in meters/sec

Thank you very much