- #1
marciokoko
Gold Member
- 87
- 0
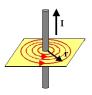
I'm reading how a charged particle moving through a magnetic field experiences a force (called magnetic force).
I understand that it moves the particle in a certain direction and because the greatest force is experienced when the magnetic field is perpendicular to the particle's velocity vector, then it keeps moving the particle in a circular motion, acting as a centripetal force.
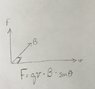
My interest is specifically to apply my calculus and trigonometry to better understand their application in a related example. So I know that F = qvBsinØ and I know that I can use calculus to calculate how the path of the particle changes as the angle and force change (this last one seems a bit more complicated).
Can someone with tons of patience help me visualize an example where I could calculate the changing force?
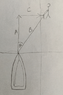
Sorry, I haven't been clear enough, first off I want to understand the trigonometry part, how the sinØ affects and is determined? So I am trying to understand why sine is used when calculating the force required to pull a boat with a rope from shore when the rope and how its affected by the angle.
I understand that it moves the particle in a certain direction and because the greatest force is experienced when the magnetic field is perpendicular to the particle's velocity vector, then it keeps moving the particle in a circular motion, acting as a centripetal force.
My interest is specifically to apply my calculus and trigonometry to better understand their application in a related example. So I know that F = qvBsinØ and I know that I can use calculus to calculate how the path of the particle changes as the angle and force change (this last one seems a bit more complicated).
Can someone with tons of patience help me visualize an example where I could calculate the changing force?
Sorry, I haven't been clear enough, first off I want to understand the trigonometry part, how the sinØ affects and is determined? So I am trying to understand why sine is used when calculating the force required to pull a boat with a rope from shore when the rope and how its affected by the angle.
Last edited: