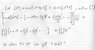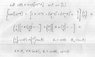Spinnor
Gold Member
- 2,227
- 419
Can a point in S^3 be uniquely labeled by a 2 component Spinor?
Thanks for any help!
Thanks for any help!