Can anyone check my working on the resultant force ,test question

[cracktheegg]

Homework Statement

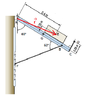
[URL=http://s1345.photobucket.com/user/Duk_Bato/media/Untitled_zps268ea812.png.html][PLAIN]http://i1345.photobucket.com/albums/p679/Duk_Bato/Untitled_zps268ea812.png[/URL][/PLAIN]

[URL=http://s1345.photobucket.com/user/Duk_Bato/media/Untitled_zpsbae78257.png.html][PLAIN]http://i1345.photobucket.com/albums/p679/Duk_Bato/Untitled_zpsbae78257.png[/URL][/PLAIN]

Homework Equations

ƩMA = Ʃ r x F
Total Force of x,y= 0

The Attempt at a Solution

bi)150(0.4)+(50)(0.3)-Fsin50(0.5)
=0

Ffb=150(0.4)+(50)(0.3)/ sin50(0.5)
=195.81N ( answer is wrong why?)

 

[TSny]

Hello, cracktheegg.

You have not calculated the cross products correctly for the torques at G and E. It's more complicated than just multiplying the forces by the given distances. Did you draw the vectors $\vec{r}$ and $\vec{F}$ for each force?

 

[cracktheegg]

bi)Moment of mass=(50)cos30 *0.3

Moment of object=(150* cos30 * 0.4

moment of GE= Fsin50(0.5)

is this correct?

 

[TSny]

The moments for the 50 N force and the unknown force look correct.

For the 150 N force, note that the position vector extends from A to E.

 

[cracktheegg]

The moments for the 50 N force and the unknown force look correct.

For the 150 N force, note that the position vector extends from A to E.

Sry, can you show me the working, i really can't visualize.

 

[TSny]

Here is the position vector $\vec{r}$ for E. You'll need to work out $\vec{r} \times \vec{F_E}$.

 

[cracktheegg]

I use 0.05/0.4
tan^-1(0.05/0.4)
0.4/cos(tan^-1(0.05/0.4))=r⃗
r⃗ * 150=60.46

I do (60.46 + (50)cos30 *0.3)/sin50(0.5)

 

[TSny]

I use 0.05/0.4
tan^-1(0.05/0.4)
0.4/cos(tan^-1(0.05/0.4))=r⃗

OK, this gives you the magnitude of $r$. (You could also have gotten this with the Pythagorean theorem).

r⃗ * 150=60.46

You need to take into account the angle θ between r and the force. M = r F sinθ.

 

[cracktheegg]

OK, this gives you the magnitude of $r$. (You could also have gotten this with the Pythagorean theorem).



You need to take into account the angle θ between r and the force. M = r F sinθ.

Thanks I finally get the answer and start to understand why

0=150cos(67.13)+50sin30+179.4cos50-Rx
0=150sin(67.13)+50cos30-179.4sin50+Ry
Should I use the above to find the magitude at hinge A?

And what does iii) mean?

 

[cracktheegg]

Can anyone help me with b iii)
I can't get the answer, I use moment to find the force

 

[TSny]

Thanks I finally get the answer and start to understand why

0=150cos(67.13)+50sin30+179.4cos50-Rx
0=150sin(67.13)+50cos30-179.4sin50+Ry
Should I use the above to find the magitude at hinge A?

It looks like you chose your x-axis along the table and y-axis perpendicular to the table. Note that the 150 N force does not make an angle of 67.13 degrees with the table. The angle of 67.13 degrees is the angle between the 150 N force and the position vector from A to E.

I think this part of the problem would be much easier if you choose your x-axis horizontal and your y-axis vertical.

 

[TSny]

Can anyone help me with b iii)
I can't get the answer, I use moment to find the force

My interpretation of this part, is that you need to find the force P of the arm that would just allow the force from the strut FB to go to zero. So, it's like part (i) except you replace the force of the strut by the force P and solve for the force P.