Can I determine mass & spring k from graph of wave, t, a, & vectors?

[michael872940]

Classical problems for hookes law generally give either mass or spring constant.

What if I have a graph of a wavelike structure that is oscillating which I can use to measure for example: T (period), t (time), Δx (displacement), v (velocity), a (acceleration) and other variables is this possible? Gravity is not a factor in this example.

I realize that graphs are different cases. The second graph is more similar to the graph I might observe. I have been using them to conceptualize this issue and try to figure out how to rearrange different equations of Force (ma, -kx) without success.

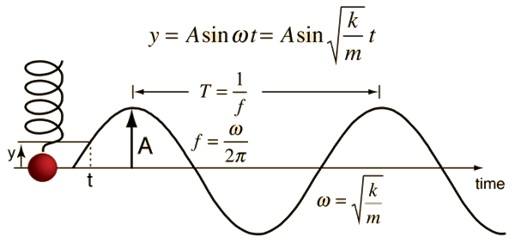
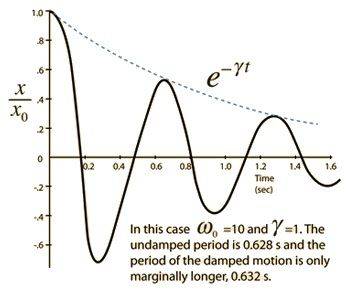
I have been thinking that the answer could be approximated by solving for M using an equation applied to pendulums

M=4π²I/gDT²

and substituting the acceleration for gravity (which is not present in this case). Even though, this is different than a pendulum, perhaps there is a vector component of acceleration that is acting on each of the turning points of the waves that that acts in a similar fashion to gravity in a pendulum. Once I find this value I could then solve for the k constant.

Alternatively, maybe I could solve for k by using Uel(x) = 1/2kx² where the points of the graph are used to plot Uel(x) and then using this value and displacement solving for k by using k= d²Uel/dx².

Is there some better solution to solve for M and K or getting the approximate answer?

 

[mjc123]

As the equation for y in the first picture tells you, the equations of motion depend on the ratio k/m. Analysing the motion can give you this ratio, but can't give you the actual values of k and m separately.