Can Linear Programming Solve Problems with Division Constraints?

AI Thread Summary
Linear programming may not directly solve problems with division constraints, as the presence of division complicates the linearity of the model. The discussion highlights that while the problem resembles standard linear programming, the division by weights raises questions about its linearity. The Simplex method is typically effective for linear problems, but the division aspect needs further consideration. Clarification on whether the weights sum to one could impact the approach taken. Overall, the feasibility of applying linear programming techniques to this problem remains uncertain.
Cheema154
Messages
1
Reaction score
0
Member warned about posting homework in non-homework section, with no effort shown
Hello,

Below is a description written in Latex.

u9UmUyP.jpg


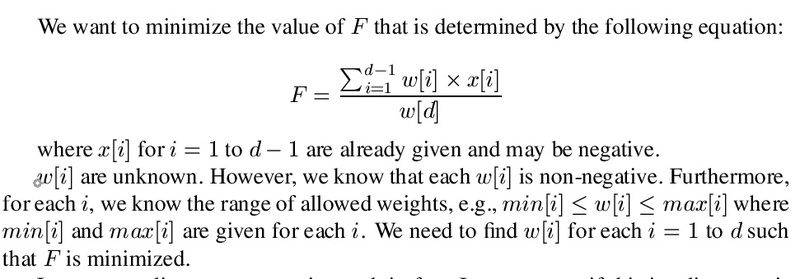
I am not sure how to solve this problem. I am new to linear programming and, in fact, I do not know if it can be solved by linear constraints.

Please guide. Thanks
 
Last edited:
Mathematics news on Phys.org
Since you call w "weights", do they sum to 1? Except for the division by w[d], this is a standard linear programming problem and the Simplex method should work. With that division, it is not immediately clear to me if it is a linear problem.
 

Thread 'What Exactly is Dirac’s Delta Function? - Insight'

Insights auto threads is broken atm, so I'm manually creating these for new Insight articles. In Dirac’s Principles of Quantum Mechanics published in 1930 he introduced a “convenient notation” he referred to as a “delta function” which he treated as a continuum analog to the discrete Kronecker delta. The Kronecker delta is simply the indexed components of the identity operator in matrix algebra Source: https://www.physicsforums.com/insights/what-exactly-is-diracs-delta-function/ by...
View full post »

Thread 'Fermat's Last Theorem'

Fermat's Last Theorem has long been one of the most famous mathematical problems, and is now one of the most famous theorems. It simply states that the equation $$ a^n+b^n=c^n $$ has no solutions with positive integers if ##n>2.## It was named after Pierre de Fermat (1607-1665). The problem itself stems from the book Arithmetica by Diophantus of Alexandria. It gained popularity because Fermat noted in his copy "Cubum autem in duos cubos, aut quadratoquadratum in duos quadratoquadratos, et...
View full post »
Thread 'Imaginary Pythagorus'

Thread 'Imaginary Pythagorus'

I posted this in the Lame Math thread, but it's got me thinking. Is there any validity to this? Or is it really just a mathematical trick? Naively, I see that i2 + plus 12 does equal zero2. But does this have a meaning? I know one can treat the imaginary number line as just another axis like the reals, but does that mean this does represent a triangle in the complex plane with a hypotenuse of length zero? Ibix offered a rendering of the diagram using what I assume is matrix* notation...
View full post »

Similar threads

B Solving Simultaneous equations with cos() and sin()
Replies
4
Views
1K
A Are these two optimization problems equivalent?
Replies
1
Views
1K
Difficult to understand the solution provided in the video (travelling salesman problem)
Replies
3
Views
2K
A Optimization problem classification
Replies
2
Views
1K
B A symmetric problem has an asymmetric solution - why?
Replies
21
Views
2K
B Are Inverse Problems More Complex Than Direct Problems in Mathematics?
Replies
13
Views
3K
I Optimization problem with multiple outputs: impossible?
Replies
6
Views
2K
Convex Optimization Without Slater Condition
Replies
1
Views
1K
I How to propagate errors through a regression & non-linear model?
Replies
8
Views
2K
I The Price of Beer - Linear Algebra Problem
Replies
44
Views
5K

Hot Threads

Recent Insights

Back
Top