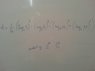diredragon
- 321
- 15
Homework Statement
For clarification a have posted the equation below as a picture file.[/B]
Homework Equations
log(a*b)= loga + logb
log(a/b) = loga-logb
log(a^n) = nloga[/B]
The Attempt at a Solution
I don't know how to start. I can't remember the rule for powering the logarithms if there is any. Any hint would do...
Its got to do something with the fact that the numbers inside the logarithms go by some sort of a rule, 3 (+3), 6 (+6), 12 (+12), 24[/B]
Attachments
Last edited: