- #1
cayusbonus
- 3
- 0
Hello,
I'm triying to solve the unidimensional heat transfer equation in transient scheme for an sphere with Crank Nicholson discretization. Because I must to obtain the Heisler Charts, I'm triying to solve the adimensional equation, that is this equation:
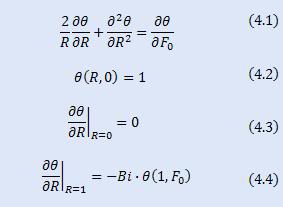 Where 4.1 is the equation, 4.2 the initial condition and 4.3 and 4.4 the boundary conditions (Neumann). In this equation, the Fo is an adimensional time, R is an adimensional radius and theta, an adimensional temperature. Then, the objective is to obtain Theta in all the grid points. The grid is the discretization of R in x-axe and Fo (time) in y-axe.
Where 4.1 is the equation, 4.2 the initial condition and 4.3 and 4.4 the boundary conditions (Neumann). In this equation, the Fo is an adimensional time, R is an adimensional radius and theta, an adimensional temperature. Then, the objective is to obtain Theta in all the grid points. The grid is the discretization of R in x-axe and Fo (time) in y-axe.
I've used the fictitious point system for implement the boundary conditions, and after a hard work, I've made this code:
With this code, I'm triying to plot the center sphere temperature evolution, this mean to plot the Theta in R=0 for all the times (Fo). But the problem is that it's not ploting correct, and my question is if you can see anything incorrrect in the code (matrix implementations, index evolutions, discretizations...). An extrange issue is that when the number of points is increased (N and M), the integration goes more and more away from the correct expected result.
Thanks.
I'm triying to solve the unidimensional heat transfer equation in transient scheme for an sphere with Crank Nicholson discretization. Because I must to obtain the Heisler Charts, I'm triying to solve the adimensional equation, that is this equation:
I've used the fictitious point system for implement the boundary conditions, and after a hard work, I've made this code:
Code:
M=8;
N=15;
DR=1/M;
DFo=0.2/N;
a=DFo/(2*DR);
hold on
for j=0.01:0.05:0.8
Bi=j;
c=-2*DR*Bi;
for m=1:M+1
dA0(m)=-1-2*a;
if m>1
dA1(m-1)=a*(1+1/(m-1));
dA_1(m-1)=a*(1-1/m);
end
end
A=diag(dA0,0)+diag(dA1,1)+diag(dA_1,-1);
A(1,1)=-1-6*a;
A(1,2)=6*a;
a1=a*(1+1/M);
a2=-1-2*a;
a3=a*(1-1/M);
A(M+1,M)=a1+a3;
A(M+1,M+1)=a1*c+a2;
for m=1:M+1
dB0(m)=1-2*a;
if m>1
dB1(m-1)=a*(1+1/(m-1));
dB_1(m-1)=a*(1-1/m);
end
end
B=diag(dB0,0)+diag(dB1,1)+diag(dB_1,-1);
B(1,1)=1-6*a;
B(1,2)=6*a;
b1=a1;
b2=1-2*a;
b3=a3;
B(M+1,M)=b1+b3;
B(M+1,M+1)=b1*c+b2;
Th=ones(M+1,N+1);
C=-inv(A)*B;
for k=1:N
Th(:,k+1)=C*Th(:,k);
end
Tita=Th(1,:);
Fo=(0:DFo:0.2);
plot(Fo,Tita)
endWith this code, I'm triying to plot the center sphere temperature evolution, this mean to plot the Theta in R=0 for all the times (Fo). But the problem is that it's not ploting correct, and my question is if you can see anything incorrrect in the code (matrix implementations, index evolutions, discretizations...). An extrange issue is that when the number of points is increased (N and M), the integration goes more and more away from the correct expected result.
Thanks.