Can One Interaction Term Represent Multiple Vertices in Feynman Diagrams?

[Josh1079]

Hi,

My question is that can one interaction term represent two vertices?

For instance, can the lagrangian interaction terms L = eψγ^μψA_μ represent a feynman diagram like these:

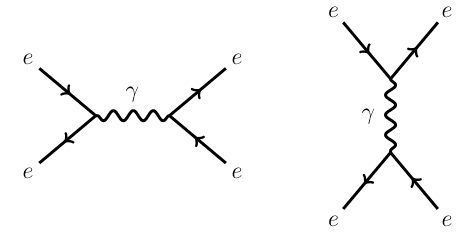
or should there be two terms in the lagrangian to construct such diagrams?

Thanks!

 

[Orodruin]

The interaction term gives you the vertices. The vertices in your two diagrams are both the same.

 

[Josh1079]

Thanks for the reply!

So I guess I can draw the same vertices several times in a diagram with the interaction term appearing only once in the Lagrangian?

 

[Orodruin]

Yes, those correspond to higher orders in perturbation theory.

 

[Josh1079]

Got it!

Thank you so much Orodruin!

 

[ChrisVer]

the lagrangian gives you the rules by which you can draw diagrams... afterall the vertices in a diagram only correspond to a coupling constant and conservation of energy/momentum.