Blockade
- 68
- 0
Can someone help me relearn finding the angle between two forces when solving for work of each forces (gravity, tension, fF, normal)?
I remember that cos(90°-α) = sin(α) but what I don't understand is when the angle in between is "90°-α" or when it's just "α". I tried doing this on my own and but my work is always wrong when calculating the angle in between for each dot product.
Problem:
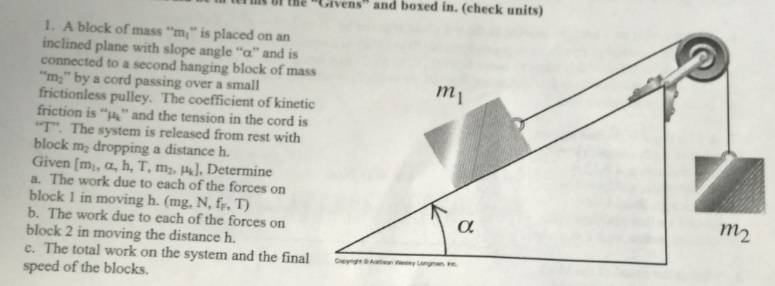
Attempt:

I remember that cos(90°-α) = sin(α) but what I don't understand is when the angle in between is "90°-α" or when it's just "α". I tried doing this on my own and but my work is always wrong when calculating the angle in between for each dot product.
Problem:
Attempt: