newguy_13
- 8
- 1
- Homework Statement
- Limit problem
- Relevant Equations
- There are none
I don't know what do do from here other than i can make the 3/e^x a 0 due to the fact its divided by such a large number. What do i do with the e^-3x? Thanks for the help
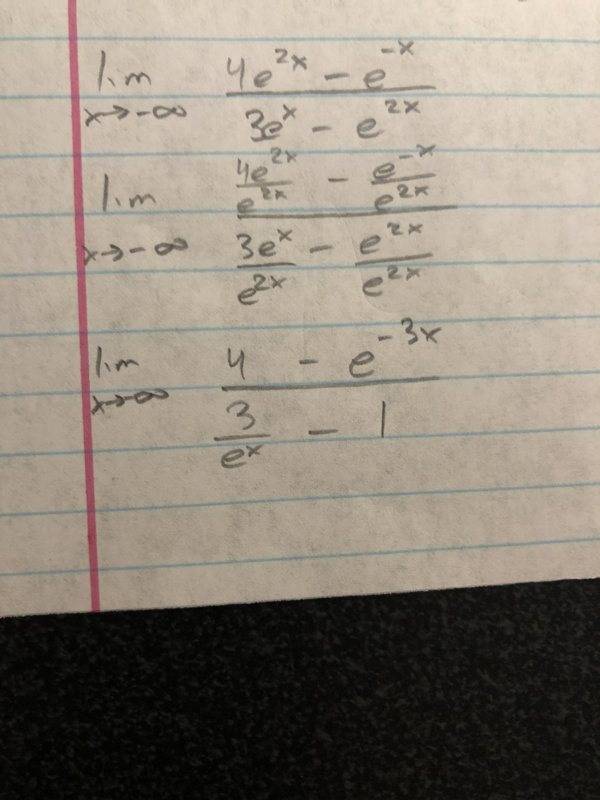
Last edited by a moderator: