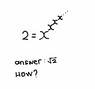High School Can someone solve this exponential equation for me?
- Thread starter Ameer Bux
- Start date
Click For Summary
The equation 2 = x^(x^(x...)) leads to the conclusion that x equals the square root of 2, approximately 1.4142135. This solution arises from recognizing that the infinite exponentiation can be simplified to x = 2^(1/x). However, the discussion highlights the complexity of exponentiation, noting that the order of operations significantly affects the outcome. It is emphasized that while the square root of 2 satisfies the equation, the reasoning behind the solution is not a formal proof. The conversation also touches on convergence conditions for exponential towers, indicating that not all values yield the same limit.
Similar threads
- · Replies 1 ·
High School
What went wrong with (-x)^2=x^2?
- · Replies 22 ·
- · Replies 2 ·
- · Replies 2 ·
- · Replies 3 ·
- · Replies 2 ·
- · Replies 3 ·
- · Replies 3 ·
High School
Bounds for the index of a radical
- · Replies 7 ·
- · Replies 13 ·