Can Symmetry Help Us Solve Simultaneous Equations with Different Variables?

[menager31]

x^{5}=5y^{3}-4z
y^{5}=5z^{3}-4x
z^{5}=5x^{3}-4y

We get five solutions (0,1,-1,2,-2) for x=y=z. But it's hard to do this when y\neqx\neqz.
Any ideas?

 

[hotvette]

These are a set of non-linear simultaneous equations. I believe numerical methods are needed.

 

[menager31]

These are a set of non-linear simultaneous equations. I believe numerical methods are needed.

:|
It wasn't hard to guess that it's non-linear. But have you got any idea?

 

[hotvette]

Well, you can try Newton's method for solving simultaneous non-linear equations. Click the link in my signature for an example.

Actually, I tried it for this problem for about 30 minutes and wasn't able to find any solution other than the ones you already know.

 

[robphy]

can you take advantage of the symmetry in x,y,z?
[you probably can see that each equation has odd powers in each of x,y, and z]

 

[HallsofIvy]

That was why he first tried x= y= z which gives the solutions cited. The question was whether itis possible to get a solution with x, y, z different. Of if it is, then those same values permuted among x, y, z is also a solution.

 

[menager31]

So, you suggest that all of acceptable values of x,y,z are only 0,1,-1,2,-2?

 

[robphy]

Maple says so [for real solutions].
I've seen a similar problem earlier... there must be a way to more methodically show that those are the only solutions for this apparently special set of symmetrical equations. If you assume that x=/=y, can it be shown that no solution with real z exists?

 

[AlephZero]

You can show these are the only solution by a semi-graphical, semi-analytical argument. (which I guess you could make it more rigorous if you want to).

The equations are
x⁵=5y³-4z (1)
y⁵=5z³-4x (2)
z⁵=5x³-4y (3)

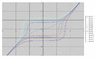
Let z be some fixed value. Then the solutions of (1) are a set of curves, where dy/dx > 0 for every curve.

Similarly the solutions of (2) are a set of curves where dy/dx < 0 everywhere.

So for a given value of z, there is at most one solution (x,y,z) of equations (1) and (2), because the solution must be the interesection of a curve with positive slope (1) and a curve with negative slope (2). Plotting out the curves with a spreadsheet shows there is a unique solution to (1) and (2) for every value of z. The solutions lie on a smooth curve in 3D space.

Plots of the (x,y) curves for (1) and (2), for z = -3, -2.5, -2, ... 2.5, 3, attached

Using the same argument, the solutions to (2) and (3) also lie on a smooth curve.

The solutions to all 3 equations are the intersections of these two curves.

It's clear (by drawing pictures) the two curves diverge for large values of z and the only solutions are x = y = z = (-2, -1, 0, 1, 2)

But this is a horrible argument, because it ignores the symmetry in the equations! Somebody do better, please!