Discussion Overview
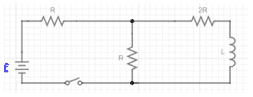
The discussion revolves around finding the total resistance and time constant in a complex star circuit involving a battery, resistor, and inductor. Participants explore different methods to analyze the circuit, including Thevenin's theorem and differential equations.
Discussion Character
- Homework-related, Technical explanation, Debate/contested
Main Points Raised
- One participant states the time constant in an RL circuit is calculated as t=L/R but struggles to find the total resistance due to the star configuration.
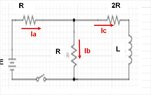
- Another participant suggests writing differential equations using Kirchhoff's laws as a formal approach to analyze the circuit.
- Some participants propose using Thevenin's theorem to find the equivalent series resistance and simplify the problem.
- A participant mentions confusion regarding the load resistor in the circuit, suggesting the inductor could be treated as the load.
- There is a discussion about the calculated Thevenin voltage and resistance, with one participant asserting that the time constant can be derived from the Thevenin equivalent circuit.
- One participant claims the time constant is 0.1s, while another later suggests it should be -0.1s, leading to a debate about the sign of the time constant.
- Participants discuss the standard format for the exponential decay factor, emphasizing that both time and the time constant are typically represented as positive quantities.
Areas of Agreement / Disagreement
Participants express differing views on the sign of the time constant, with some asserting it should be positive while others suggest it could be negative. The discussion remains unresolved regarding the interpretation of the time constant.
Contextual Notes
There are unresolved assumptions about the circuit configuration and the definitions of terms like load resistor and time constant. The discussion reflects varying levels of understanding among participants regarding the application of Thevenin's theorem and the mathematical representation of the time constant.