Happiness
- 686
- 30
I don't fully understand the argument below used to derive the Lorentz transformation equation ##y'=y##.

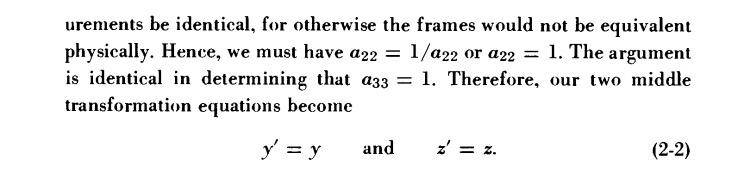
Suppose we have a rod of unit length placed stationary in frame S. According to an observer in frame S' (which is moving at a velocity v relative to frame S), this rod is moving and its length would be ##\frac{1}{\gamma}## (i.e., ##\Delta l'=\frac{\Delta l}{\gamma}=\frac{1}{\gamma}##).
Following the above argument, we now place the rod stationary in frame S'. The rod must also be of unit length in frame S'; otherwise there would be an asymmetry in the frames. In this case, however, the S-observer would measure the rod's length to be ##\gamma## (i.e., ##\Delta l=\gamma\Delta l'=\gamma\times1##). Now, because of the reciprocal nature of these length measurements, the first postulate (see below) requires that these measurements be identical, for otherwise the frames would not be identical physically. Hence, we must have ##\gamma=\frac{1}{\gamma}## or ##\gamma=1##.
But for non-zero v, ##\gamma\neq1##. Hence, I don't understand the above argument fully.
Of course, I know my argument involving ##\Delta l## is wrong. What I don't understand is why the argument works for ##y## but not for ##\Delta l##.

Suppose we have a rod of unit length placed stationary in frame S. According to an observer in frame S' (which is moving at a velocity v relative to frame S), this rod is moving and its length would be ##\frac{1}{\gamma}## (i.e., ##\Delta l'=\frac{\Delta l}{\gamma}=\frac{1}{\gamma}##).
Following the above argument, we now place the rod stationary in frame S'. The rod must also be of unit length in frame S'; otherwise there would be an asymmetry in the frames. In this case, however, the S-observer would measure the rod's length to be ##\gamma## (i.e., ##\Delta l=\gamma\Delta l'=\gamma\times1##). Now, because of the reciprocal nature of these length measurements, the first postulate (see below) requires that these measurements be identical, for otherwise the frames would not be identical physically. Hence, we must have ##\gamma=\frac{1}{\gamma}## or ##\gamma=1##.
But for non-zero v, ##\gamma\neq1##. Hence, I don't understand the above argument fully.
Of course, I know my argument involving ##\Delta l## is wrong. What I don't understand is why the argument works for ##y## but not for ##\Delta l##.



