Capacitance approximation of a non parallel plate capacitor

[spyrustheviru]

I am in process of designing a homemade capacitance sensor and I'd like to have an approximation of the resulting capacitance of the following geometry.
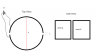
The plates are placed on the outer surface of a food grade plastic cylinder. The distance z between their edges is many times smaller than the diameter d of the cylinder (z<<d). Each plate has an area of A and it's dimentions are comparable to d, but, according to what I have in mind, smaller.
the dielectric is air.
is there any approximate value as a function of A and d that I could use to determine the sizes at which this geometry would produce a measurable capacitance?

i am away from my books and the calculation method escapes my mind right now (plus, this is more complex than anything we did on the respective course), I'd appreciate any help. It is not crucial to have an analytical formula, but something to give me an idea of what to expect depending on the dimentions used.

 

[mfb]

I don't understand your side view. If both plates cover (nearly) 50% of the cylinder, how do you get this side view?

I would expect that capacitance depends significantly on the gap of z and the edges of the plates, if z<<d.

 

[Baluncore]

There are many ways of measuring capacitance. No matter what values of A and d you use it will produce a measurable capacitance. Maybe build an oscillator with this as the tuning capacitor. Measure the frequency, compute the capacitance. I would guess about 25 pF for your geometry and tupperware size. If your geometry diagram was better defined it would be possible to come up with an equation. The axial separation of the near edges or corner clearance will be critical.

 

[spyrustheviru]

to make the geometry more clear:
think of a hollow plastic cylinder. we take a metal sheet and place it on the walls of this cylinder. then we cut 2 fine strips of it (with a width of z, as noted) on two opposite points (as shown on the top view). The side view is accurate, supposing we look at it placing one of those two strips directly in the center of our view.

25pF is a good starting point I believe. How greater would this be if the cylinder was long and narrow (ie, d being quite smaller than the largest dimention of area A, something like 5mm versus 15-20cm)?
would the variations of this capacitance, caused by the variation of the dielectric, be greater? (it would help detection greatly if they were)

 

[mfb]

Okay, so the height of the cylinder is the height of the side view.
Good, that is the geometry I had in mind.

Capacitance is roughly proportional to the height of the cylinder. The influence of a changing d will depend on z and the structure of that gap.

 

[Baluncore]

A very thin walled conductive tube, of diameter d and length y, is divided by a plane that contains it's axis with a cut of width z. Assuming it is filled with, and surrounded by air, what is the capacitance between the two parts isolated by the cut.

We know that the close edges will be most important so we can treat the problem as the capacitance between two parallel strips. I let the external curve cancel the effect of the internal curve. Yes, I know it is crude, but it does avoid Elliptic Integral ratios and Schwarz-Christoffel transformation.

There are two of these close gaps of separation s, so we will treat the strips as having widths equal to a quadrant of the cylinder circumference, then double the result.

Now, this thread; https://www.physicsforums.com/showthread.php?t=130876 gives us the following; The capacitance between adjacent strips having a thickness, t, width, w, and separation, s, laying on a dielectric with constant, k, is approximately given by,

C(pf/cm) = 0.12t/w + 0.09(1+k) Log_10(1 + 2w/s + w^2/s^2).

The thickness is << separation so the first term can be zero.
We are in air so dielectric constant k takes a value of one.
w = Pi * d / 4, a quadrant of the surface.
So the equation becomes... all measured in cm...

C(pf) = 2 * y * 0.18 * Log10 ( 1 + 2*w/s + w^2/s^2).

As a check we calculate for a diameter = 20 cm, so w = 20 * Pi / 4
length y = 15 cm, with gap z = s = 0.1 cm

Trivial source code in BASIC.
Dim As Double pi = 4 * Atn(1)
Dim As Double d = 20 ' diameter cm
Dim As Double w = Pi * d * 0.25 ' quadrant of cylinder
Dim As Double s = 0.1 ' separation cm
Dim As Double y = 15 ' length cm
Dim As Double pF ' capacitance
pF = 2 * y * 0.18 * Log( 1 + 2*w/s + w^2/s^2) / Log(10)
Print pF ' 23.75 pF

After 40 years of practice in the field, my feeling of 25 pF is probably pretty close. It suggests that the “coplanar strips” model I have developed here is a reasonable approximation.

Now you can put the thickness term back in if you want, or study the sensitivity to variation of z.

 

[the_emi_guy]

Use Fastcap (http://www.fastfieldsolvers.com/). Its free.