- #1
SadStudent
- 7
- 0
Homework Statement
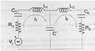
Given a set of two capacitively coupled RLC circuits where each has a capacitor [itex]C[/itex] and they share a coupling capacitor [itex]C^{'}[/itex].
I'm trying to find nice organized material that will explain the various relevant
coefficients\concepts like [itex]QF[/itex], bandwidth etc. in relation to the above mentioned setup.
Or how to find the function of the maximal voltage as the function of frequency given a certain setup.
Homework Equations
The Attempt at a Solution
I do know how to solve the differential equations involved and get the voltage and current as the function of time but I can't find good sources that could explain all the aspects of coupling two circuits using a capacitor.
Last edited: