vissh
- 82
- 0
HeyoO everyone (^_^) and Thanks for your time.
This question is about the "intial" point of time i.e. as soon as the key is closed.
Before the current starts to flow which charges the capacitor till the voltage of capacitor is equal to voltage across the battery.
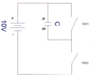
A capacitor,C is directly connected to a DC battery of (say) 10V.
If the plates of the capacitor are taken to be at 0V, then what would be potential of "negative" and "positive" terminal
of battery relative to the plates?
Electrons likes to flow from "Low" to "High" potential.
Finally, the plate A will be "Positively" charged and plate B will be negatively charged.
That means Electrons flowed from A -> X -> Positive terminal -> Negative terminal -> Y -> B which created those charges on Plate A and B.
This implies that Initially (the time at which this question is to be answered) Plate A [ 0V ] was at a lower potential than the positive terminal of the battery... And... Plate B [ 0V] was at a higher potential than the negative terminal of the battery.
A battery is of 10V implies that the potenital difference between the +ve and -ve terminal is of 10V.
I think that the +ve terminal will be at +5V and -ve terminal will be at -5V.
That is +"Half of the voltage" on positive terminal and -"half of voltage" on negative terminal.
[Q.01] Am i right ( ) ??
) ??
[Q.02] Will other pairs of (+ve Terinal , -ve terminal) work out?? :
Like (+9V , -1V) or (+4V, -6V).
[Q.03] The pair (+13V , +3V) will not be correct right ??
Homework Statement
This question is about the "intial" point of time i.e. as soon as the key is closed.
Before the current starts to flow which charges the capacitor till the voltage of capacitor is equal to voltage across the battery.
A capacitor,C is directly connected to a DC battery of (say) 10V.
If the plates of the capacitor are taken to be at 0V, then what would be potential of "negative" and "positive" terminal
of battery relative to the plates?
Homework Equations
Electrons likes to flow from "Low" to "High" potential.
Finally, the plate A will be "Positively" charged and plate B will be negatively charged.
That means Electrons flowed from A -> X -> Positive terminal -> Negative terminal -> Y -> B which created those charges on Plate A and B.
This implies that Initially (the time at which this question is to be answered) Plate A [ 0V ] was at a lower potential than the positive terminal of the battery... And... Plate B [ 0V] was at a higher potential than the negative terminal of the battery.
A battery is of 10V implies that the potenital difference between the +ve and -ve terminal is of 10V.
The Attempt at a Solution
I think that the +ve terminal will be at +5V and -ve terminal will be at -5V.
That is +"Half of the voltage" on positive terminal and -"half of voltage" on negative terminal.
[Q.01] Am i right (
[Q.02] Will other pairs of (+ve Terinal , -ve terminal) work out?? :
Like (+9V , -1V) or (+4V, -6V).
[Q.03] The pair (+13V , +3V) will not be correct right ??