Car on the banked turn with friction

[Mehtab]

Homework Statement

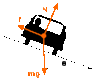
Car traveling along the "reverse" banked turn (road tilted away from the curvature). Radius of curvature is 15 m, static friction between road and tires is 0.5, and banking angle is 10 degrees. Find the maximum velocity possible on this reverse banked turn.

Homework Equations

v=sqrt(Usgr)

The Attempt at a Solution

sqrt(0.5 x 9.8 x 15)= 8.57 m/s

Its wrong as actual answer is 7.2m/s

 

[pat666]

i get 7.8m/s..

 

[Mehtab]

i get 7.8m/s..

how?

 

[Mehtab]

I have tried and got answer using this equation:
v=sqrt(((MUcostheta-sintheta) x g x r)/(costheta-MUsintheta))

I derived it by:
sum of x forces: Fx=Fcostheta-MU(Nsintheta)=(mv)^2/r
sum of y forces: Fy=0=Ncostheta-MU(Nsintheta)-mg
mg=N(costheta-MU(sintheta)
N=(mg)/(costheta-MU(sintheta))

Netforce: -Fnet(opposite direction)=Nsintheta-fcostheta(Opposite direction)
Fnet=-Nsintheta+MU(Ncostheta)
=N(-sintheta+MU(costheta))
=((mg)/(costheta-MU(sintheta)) x (-sintheta+MU(costheta)
Fnet=Fcentripetal

(mv^2)/r=((mg)/(costheta-MU(sintheta)) x (-sintheta+MU(costheta)
v=sqrt((MUcostheta-sintheta) x g x r)/(costheta-MUsintheta))