Goldenwind
- 145
- 0
[SOLVED] Cart on an inclined ramp, with rebound
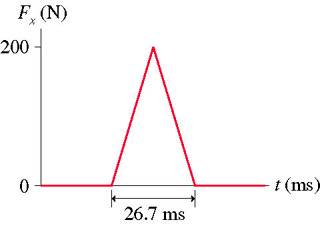
A 500 g cart is released from rest 1.0 m from the bottom of a frictionless, 30° ramp. The cart rolls down the ramp and bounces off a rubber block at the bottom. The figure (below) shows the force during the collision.
After the cart bounces, how far does it roll back up the ramp?
It'd be cool if we could get this solved relatively soon. It's due at midnight EST. And no, I'm not going to be a jerk if it's not solved by then, it's my fault for leaving it late :)
In theory, I have this solved, but I've made a mistake somewhere as it says my answer is wrong. This is what I did:
m = 500g = 0.5kg
x = 1.0m
\theta = 30°
Starting from rest, the cart travels 1.0m at the acceleration of gravity (Altered by the incline of the ramp).
v_f^2 = v_i^2 + 2ad
Assuming that downwards is the negative direction, therefore v_f and g will be negative.
If the incline was 90°, the cart would freefall.
If the incline was 0°, the cart wouldn't be affected by gravity at all.
Therefore, we need a coefficient on g. Since sin(90) = 1 (Full gravity) and sin(0) = 0 (No effect), we use sin(30) = 0.5 to make this alteration.
v_f = \sqrt{0 + 2ad}
v_f = -\sqrt{2(sin(30)g)d}
sin(30) = 0.5, which cancels out the 2. g = 9.8, and d = 1.0 so can be ignored.
v_f = -\sqrt{g} = -3.1305
This is the speed of the cart immediately before it hits the rubber block.
Next, J = F\Delta t = \Delta P
F\Delta t = 200 * \frac{26.7}{1000} = 5.34 Ns
5.34 Ns = \Delta P = | mv_0 - mv_f |
Where v_0, v_f are the velocities immediately before and after rebounding, respectively.
The velocity before rebounding, v_0[/tex], we just calculated to be -3.1305 (The v_f of rolling down the ramp).<br /> <br /> 5.34 Ns = | 0.5 * -3.1305 - 0.5 * v_f |<br /> 5.34 Ns = | -1.56525 - 0.5*v_f |<br /> For the absolute value to equal 5.34, what is inside of the absolute bars must be 5.34, or -5.34. The only way for it to become 5.34 is if v_f is large enough to bring -1.56525 above positive, and into 5.34 (Meaning v_f would need to be somewhere around 12m/s, which doesn't make sense, as that would imply it actually gained speed in rebounding).<br /> <br /> So, we assume the absolute bars to be equal to -5.34, and solve v_f accordingly.<br /> -5.34 Ns = -1.56525 - 0.5*v_f<br /> v_f = \frac{-5.34 + 1.56525}{0.5}<br /> v_f = -7.55<br /> Since v_f is a rebound up the incline, it is taken to be a positive value, 7.55m/s.<br /> This is also above our initial collision value of 3.13, which also isn't possible, so my mistake is probably before this point.<br /> <br /> However, just to solve the problem (And to show how to do so):<br /> v_0, v_f now respectively represent the velocity just as you begin your rebound, and the velocity just as you finish your rebound (Once gravity has slowed the cart back down to 0m/s, before it begins falling down the ramp again)<br /> v_f = v_i + at<br /> 0 = 7.55 + (-sin(30)gt)<br /> 7.55 = 0.5*9.8t<br /> t = 1.54 sec<br /> <br /> And lastly, finding out how far the cart can recoil in 1.54 seconds, with an initial speed of 7.55m/s and a gravitational force of -sin(30)g on it.<br /> d = \frac{v_i + v_f}{2} * t<br /> d = \frac{7.55 + 0}{2} * 1.54<br /> d = 5.82m<br /> <br /> By the grading system, I'm told this answer is wrong. This makes sense too, as it shouldn't rebound farther than it initially started. My error is most likely in calculating the 7.55m/s.
A 500 g cart is released from rest 1.0 m from the bottom of a frictionless, 30° ramp. The cart rolls down the ramp and bounces off a rubber block at the bottom. The figure (below) shows the force during the collision.
After the cart bounces, how far does it roll back up the ramp?
It'd be cool if we could get this solved relatively soon. It's due at midnight EST. And no, I'm not going to be a jerk if it's not solved by then, it's my fault for leaving it late :)
In theory, I have this solved, but I've made a mistake somewhere as it says my answer is wrong. This is what I did:
m = 500g = 0.5kg
x = 1.0m
\theta = 30°
Starting from rest, the cart travels 1.0m at the acceleration of gravity (Altered by the incline of the ramp).
v_f^2 = v_i^2 + 2ad
Assuming that downwards is the negative direction, therefore v_f and g will be negative.
If the incline was 90°, the cart would freefall.
If the incline was 0°, the cart wouldn't be affected by gravity at all.
Therefore, we need a coefficient on g. Since sin(90) = 1 (Full gravity) and sin(0) = 0 (No effect), we use sin(30) = 0.5 to make this alteration.
v_f = \sqrt{0 + 2ad}
v_f = -\sqrt{2(sin(30)g)d}
sin(30) = 0.5, which cancels out the 2. g = 9.8, and d = 1.0 so can be ignored.
v_f = -\sqrt{g} = -3.1305
This is the speed of the cart immediately before it hits the rubber block.
Next, J = F\Delta t = \Delta P
F\Delta t = 200 * \frac{26.7}{1000} = 5.34 Ns
5.34 Ns = \Delta P = | mv_0 - mv_f |
Where v_0, v_f are the velocities immediately before and after rebounding, respectively.
The velocity before rebounding, v_0[/tex], we just calculated to be -3.1305 (The v_f of rolling down the ramp).<br /> <br /> 5.34 Ns = | 0.5 * -3.1305 - 0.5 * v_f |<br /> 5.34 Ns = | -1.56525 - 0.5*v_f |<br /> For the absolute value to equal 5.34, what is inside of the absolute bars must be 5.34, or -5.34. The only way for it to become 5.34 is if v_f is large enough to bring -1.56525 above positive, and into 5.34 (Meaning v_f would need to be somewhere around 12m/s, which doesn't make sense, as that would imply it actually gained speed in rebounding).<br /> <br /> So, we assume the absolute bars to be equal to -5.34, and solve v_f accordingly.<br /> -5.34 Ns = -1.56525 - 0.5*v_f<br /> v_f = \frac{-5.34 + 1.56525}{0.5}<br /> v_f = -7.55<br /> Since v_f is a rebound up the incline, it is taken to be a positive value, 7.55m/s.<br /> This is also above our initial collision value of 3.13, which also isn't possible, so my mistake is probably before this point.<br /> <br /> However, just to solve the problem (And to show how to do so):<br /> v_0, v_f now respectively represent the velocity just as you begin your rebound, and the velocity just as you finish your rebound (Once gravity has slowed the cart back down to 0m/s, before it begins falling down the ramp again)<br /> v_f = v_i + at<br /> 0 = 7.55 + (-sin(30)gt)<br /> 7.55 = 0.5*9.8t<br /> t = 1.54 sec<br /> <br /> And lastly, finding out how far the cart can recoil in 1.54 seconds, with an initial speed of 7.55m/s and a gravitational force of -sin(30)g on it.<br /> d = \frac{v_i + v_f}{2} * t<br /> d = \frac{7.55 + 0}{2} * 1.54<br /> d = 5.82m<br /> <br /> By the grading system, I'm told this answer is wrong. This makes sense too, as it shouldn't rebound farther than it initially started. My error is most likely in calculating the 7.55m/s.
Last edited: