Center of Gravity, objects in eqm

[Buddha]

Hey guys, I was assigned a bunch of questions by my teacher and I'm having trouble with these two:

A person is sitting with one leg outstretched, so that it makes an angle of 30 degrees with the horizontal, as the drawing indicates. The weight of the leg below the knee is 44.5 N with the center of gravity located below the knee joint. The leg is being held in this position because of force M applied by the quadriceps muscle, which is attached 0.100 m below the knee joint. Obtain the magnitude of M.

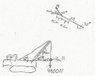
A wrecking ball (weight=4800N) is supported by a boom, which may be assumed to be uniform and has a weight of 3600N. As the drawing shows, a support cable runs from the top of the boom to the tractor. The angle between the support cable and the horizontal is 32 degrees, and the angle between the boom and the horizontal is 48 degrees. Find the tension in the support cable and the magnitude of the force exerted on the lower end of the boom by the hinge.

Hopefully the pictures show up...

 

[Pyrrhus]

Apply Equilibrium conditions

\sum_{i}^{n} \vec{F}_{i} = 0

\sum_{i}^{n} \vec{\tau}_{i} = 0

A good trick for the \tau is selecting an origin which elimnates the most forces, or unknown variables.

 

[Buddha]

It's been a long time since I've had to do this stuff...
For that first question here is what I've got (let the 44.5 N = X):
ET = My - Xy = 0
My = Xy
Mcos65 = 445cos30
M = 445cos30/cos65
M = 911.89 N
But M should equal 228 N, did I use the wrong angles or am I doing everything wrong?

 

[Pyrrhus]

You're forgetting

\vec{\tau} = \vec{F} \times \vec{r}

where |\vec{\tau}| is \tau = |\vec{r}||\vec{F}|sin\theta

where theta is the angle between the radius vector and the force vector.

or \tau = Fd where d is perpendicular to the line of action of the force.

 

[Buddha]

ah crap, thanks, you're right, so it should have been
M = 445cos30(0.25) / [cos65(.1)] = 2279.7 N
But my answer is still off by a multiple of 10, or did I just copy the answer down wrong?

 

[Pyrrhus]

It's 44.5 N not 445 N.

 

[Buddha]

haha, oops, I feel like an idiot, thanks for all the help, hopefully I don't make stupid mistakes like this when it's time for a test.

 

[Pyrrhus]

In my opinion, solve problems algebraicly then plug in the values, it avoids this kind of errors.