Center of mass and cross product

[minidee]

Let vectors vec{A}=(0,0,-3), vec{B}=(2,0,0), and vec{C}=(0,1,1).
Calculate the following, expressing your answers as ordered triples (three comma-separated numbers).

Calculate A x C. For this part, remember that only perpendicular components contribute to the cross-product. The vector C has two components--one perpendicular to vector A, and one parallel to vector A The one that is parallel is not included in the cross product.

Vector A x Vector C =


i don't even know where to start with this problem. I already did A X B but I'm not sure how to do this perpendicular parallel thing. Please elaborate and solve out the problem! Thanks!





And this center of mass problem confuses me.
Would the base of the irregular object be B, so the center of mass should be C since it is directly over it?

The abstract sculpture shown in the figure can be placed on a horizontal surface without tipping over. Different parts of the sculpture may be hollow or solid, or made of different materials, but the artist isn't revealing any such information.

Five locations labeled A through E are indicated on the diagram. Which of these, if any, is a possible location of the object's center of mass?

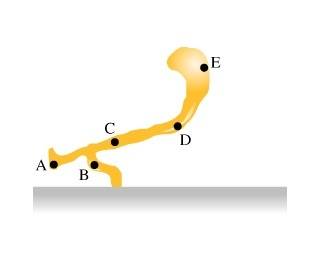
A
B
C
D
E
cannot be determined




And lastly, this problem, I've used a valid equation, got 23 degrees but the machine still churns out that my answer is wrong? What might you guys get?

A 35-cm-diameter phonograph record is dropped onto a turntable being driven at 33 and 1/3rpm. If the coefficient of friction between the record and turntable is 0.20, how far will the turntable rotate between the time when the record first contacts it and when the record is rotating at the full 33 and 1/3 rpm? Assume that the record is a homogeneous disk. Hint: You'll need to do an integral to calculate the torque.
Express your answer using two significant figures.

answer: theta= ? degrees

I think the answer is 23 degrees, I don't know why the machine says I'm wrong.

 

[Dr.D]

If you can do AxB, then do AxC the same way and don't worry about the rest of the statement.

Your figure on the CM question makes no sense to me, so I have nothing to tell you there.

For the phonograph record problem, how did you work it? Show your work.

 

[minidee]

I got total torque by integration then did work energy theorem for theta.

3(0.15 m)(33 1/3 pie/30 s)^2
divided by 8(0.19)(9.8 m/s2)
= 0.368 rad = 21.1◦.

I basically did this and got 23 degrees plugging in different numbers. but the machine says its wrong.

thanks for the help!

 

[Dr.D]

When I asked you to show your work, I did not mean the numbers so much as to show me how you set the problem up. what equations did you write?

From what you have presented, it looks like you did not write any equations at all, and that is a problem. You need to start working the problems out in symbols, writing equations and operating on those equations a step at a time to get a solution before you ever put any numbers in at all. What you have given me here is just about meaningless.

 

[minidee]

I figured out the problem. The textbook and the online software used different equations for moment of inertia. the textbook used the circular object one with 1/2mr^2 and the online software put mr^2. I can't believe I fussed over this because of some disagreement between the book and online homework grader. anyway thanks for your time!