Center of mass with one object moving

[DrummingAtom]

Homework Statement

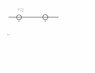
Two objects are on a stick where one is stuck in place and the other one can slide. Both objects have the same mass and the stick has negligible mass.

Homework Equations

COM = \frac{m_1 x_1 + m_2x_2}{m_1+m_2}
v_1 = t

The Attempt at a Solution

COM = \frac{m_1 \int v_1 + m_2x_2}{m_1+m_2}

Would this be correct assuming that the starting point for measuring x₁ and x₂ would be the left side? Thanks

 

[RoshanBBQ]

I would be a little careful here. You need to know the initial position of the moving mass:
\frac{m_1\left (\int v_1(t) \,dt +x_1(0) \right ) + m_2x_2}{m_1+m_2}
where x_1(t) is a function of time and x_1(0) is the constant of integration.

 

[DrummingAtom]

I would be a little careful here. You need to know the initial position of the moving mass:
\frac{m_1\left (\int v_1(t) \,dt +x_1(0) \right ) + m_2x_2}{m_1+m_2}
where x_1(t) is a function of time and x_1(0) is the constant of integration.

Thanks for responding. Ahh yes good point. Adding your part, would that be correct? I just made up the problem which is why I'm a little unsure of the conceptual part.

 

[RoshanBBQ]

Thanks for responding. Ahh yes good point. Adding your part, would that be correct? I just made up the problem which is why I'm a little unsure of the conceptual part.

I believe it is all right. The equation gives the center of mass as a function of time.

 

[DrummingAtom]

Ok cool. Thanks for your help. By the way.. Roshan from DotA?

 

[RoshanBBQ]

Ok cool. Thanks for your help. By the way.. Roshan from DotA?

Yes. DotA 2 now.