Centre of mass Momentum problem-Two blocks

[Tanya Sharma]

Homework Statement

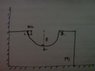
A symmetric block of mass M1 with a groove of hemisphere shape of radius R rests on a smooth horizontal surface in contact with the wall as shown in the figure. A small block of mass m2 slides without friction from the initial position .Find the maximum velocity of the block M1.Describe the motion of both the blocks M1 and m2. ( M1=100 Kg m2=10kg R=5m g=10m/s2).

Homework Equations

The Attempt at a Solution

Initially m2 is is at 1 and slides down to 2 .Since M1 has a wall towards its left side ,the wall exerts a force on M1 till m2 reaches 2 because m2 pushes against M1.So momentum of two block system can not conserved till m2 reaches 2.Afterwards , momentum can be conserved taking initial momentum when m2 is at 2.

Velocity of m2 at 2 can b found using conservation of energy between points 1 and 2.

Loss of potential energy = Gain in Kinetic energy

velocity of m2 at 2 = 10m/s

Now I have a doubt here when block m2 moves from 2 to 3...If we consider only m2 then kinetic energy of m2 at 2 should completely convert in Potential energy at 3 which gives the height to which the block rises i.e R. This means block m2 moves back and forth between 1 and 3.

But if conservation of momentum is applied then as block m2 moves from 2 to 3 the block M1 also moves ie when m2 reaches 3 then M1 is moving and m2 is at rest w.r.t M1

Applying conservation of energy

Loss in Kinetic energy of m2 =Gain in potential energy of m2 + gain in kinetic energy of (M1+m2).

This gives height to which block m2 rises less than R .

Why two different results...

Where am I getting it wrong?

 

[NoPoke]

try solving the problem without the wall in place.

 

[TSny]

Hello.

Now I have a doubt here when block m2 moves from 2 to 3...If we consider only m2 then kinetic energy of m2 at 2 should completely convert in Potential energy at 3 which gives the height to which the block rises i.e R. This means block m2 moves back and forth between 1 and 3.

But, as you later noted, m1 will be moving when m2 reaches max height after passing 2. So, not all of the kinetic energy of m2 will be converted into potential energy when m2 reaches max height. Does m2 reach 3?

See if you can conceptually see where m2 will be when m1 has its max speed. Hint: As m2 is sliding up after passing 2, what direction does it push on m1? As m2 slides back down toward 2, what direction does it push on m1? (Consider horizontal component of force.)

 

[Tanya Sharma]

But, as you later noted, m1 will be moving when m2 reaches max height after passing 2. So, not all of the kinetic energy of m2 will be converted into potential energy when m2 reaches max height. Does m2 reach 3?

No...Not all of kinetic energy is converted in potential energy .Some of it will be converted in kinetic energy gained by both m1 and m2.

That means m2 will not reach 3.The height reached will be less than R.

See if you can conceptually see where m2 will be when m1 has its max speed. Hint: As m2 is sliding up after passing 2, what direction does it push on m1? As m2 slides back down toward 2, what direction does it push on m1? (Consider horizontal component of force.)

It seems that the max speed of m1 will be when m2 slides back down to 2.

Am I correct in my assessment ?

 

[rcgldr]

It seems that the max speed of m1 will be when m2 slides back down to 2. Am I correct in my assessment ?

Yes, while m2 is between 2 and 3 there's a horizontal component of force on m1 that accelerates it. Once m2 returns back past 2, it starts slowing down m1.

 

[Tanya Sharma]

Okay...then conserving energy between 2 sliding up and 2 sliding down

$\frac{1}{2}m(v_2)^2=\frac{1}{2}m(V_{max}-v_{2,ret})^2+\frac{1}{2}M(V_{max})^2$


and conservation of momentum between points 2 up and 2 down gives

$mv_2=m(V_{max}-v_{2,ret})+MV_{max}$

Am i right?

 

[ehild]

Explain your notations, please.

ehild

 

[Tanya Sharma]

These are the notations

m=mass of smaller block

M=mass of bigger block

$v_2$ = velocity of smaller block at position 2 while going up

$V_{max}$= velocity of bigger block while smaller block is sliding back down at 2

I feel the maximum velocity bigger block can have is at 2 hence $V_{max}$

$v_{2,ret}$=velocity of smaller block while sliding back down at 2

 

[ehild]

So you mean that v2 is the velocity of the small block at point 2 when it arrived from point 1, and v2,ret is its velocity at the same deepest point when arrived from the opposite direction. Are they meant with respect to the big block or with respect to the ground?

 

[Tanya Sharma]

So you mean that v2 is the velocity of the small block at point 2 when it arrived from point 1, and v2,ret is its velocity at the same deepest point when arrived from the opposite direction.

Yes

Are they meant with respect to the big block or with respect to the ground?

w.r.t the bigger block

 

[ehild]

OK. It looks plausible that the big block has the greatest velocity when the small one is in position 2 and moving backwards. Accepting it, your equations are correct (v2ret meaning the magnitude of the velocity with respect to the big block). Determine Vmax.

ehild

 

[Tanya Sharma]

I am getting two values of Vmax . Vmax = 0 , 20/11 . Why one of the values is zero ? Is it the value of bigger block when the smaller block is passing through 2 for the first time ?

ehild...Can you explain what is the role of the wall in this problem ? Is the force of the wall responsible that we cannot conserve momentum between points 1 and 2 and only after 2 the momentum is conserved as the wall force stops acting after 2?

Am I write in my assessment that bigger block will move only after block 2 moves past 2?

 

[ehild]

That is very good, Tania. The zero velocity is valid when the small block comes from position 1. The wall can exert force only to the right. So the big block will not move till the small one pushes it towards the wall, as the two opposite forces cancel. As soon as the small block passes point 2, it pushes the big block forward. The wall can not pull it back, so the big block loses contact with the wall, and without external horizontal force, the horizontal component of momentum is conserved.

ehild

 

[Tanya Sharma]

ehild...Thank you very much

 

[TSny]

This might help. Looking at the attachment, would there be any difference in the final velocities of the 3 elastic collisions shown? [Edit: Sorry, I switched the notation for m1 and m2 so I have m1 as the small block.]

 

[Tanya Sharma]

This might help. Looking at the attachment, would there be any difference in the final velocities of the 3 elastic collisions shown?

No...In all the three cases the final velocities will be the same

Tsny...Thank you very much