Charge Induction: Understanding Electric Field Effects

[Saitama]

Homework Statement

This is no homework question, i am only trying to clear my concepts.
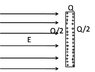
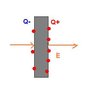
Lets say i have a conducting rod placed vertically. I give it a charge Q. The charge would stay on the outer surface. The charge will distribute equally over the surface. What would happen if i place the charged rod in an electric field of magnitude E?
(see attachment)

Homework Equations

The Attempt at a Solution

I think the negative charge will get concentrated on the left side of rod and the positive charge on the right side. But is it possible to find the amount of charge which will shift to the left and right faces or rather, the final charges on both the faces?

Any help is appreciated!

 

[Infinitum]

The Attempt at a Solution

I think the negative charge will get concentrated on the left side of rod and the positive charge on the right side. But is it possible to find the amount of charge which will shift to the left and right faces or rather, the final charges on both the faces?

There is no 'net negative' charge. The only excess charge is the +Q you put on the conductor. Now this conductor will always have a zero field inside it. So in presence of an electric field, the charges in the conductor(including the charge that it naturally possesses) will be rearranged in whatever way, so that net field inside remains zero.

I'm not sure how you can calculate the final charges on both faces, as charges of the native conductor also participate in the distribution.

 

[I like Serena]

Hi Pranav!

You make it a bit difficult when you use a rod...

But suppose you use a conducting plate that is perpendicular to your electric field E, with some surface area A.

Then inside the plate the electric field generated by the charge in the plate will neutralize your electric field E.
Suppose ΔQ is the difference in charge on the left and right sides of the plate.
Then the electric field inside is ΔQ/A which will be equal to E.
So ΔQ=EA.

 

[Infinitum]

You make it a bit difficult when you use a rod...

Hi ILS!

This is where I was unsure of exact distribution. But still, for understanding, can you please describe how the distribution can be calculated if it were a rod? A brief idea will do

 

[Saitama]

Thank you both for the replies!

@ILS: I think the electric field inside the plate should be ΔQ/Aε_o, you seem to have miss the ε_o.

 

[ehild]

It is not an easy problem. Putting a conducting body in an electric field, it redistributes the charge on the conductor, and the charge distribution on the body - either having a net charge or not - influences the field near itself. The external electric field produces such surface charge distribution that the surface of the conductor becomes equipotential. This also means that the lines of the resultant field are perpendicular to the surface. And the relation of the surface charge density σ and the resultant electric field E_r at a place is σ = ε₀E_r
And of course, the electric field inside the conductor is zero.

ehild

 

[I like Serena]

Thank you both for the replies!

@ILS: I think the electric field inside the plate should be ΔQ/Aε_o, you seem to have miss the ε_o.

Yep. Well spotted! :)

Hi ILS!

This is where I was unsure of exact distribution. But still, for understanding, can you please describe how the distribution can be calculated if it were a rod? A brief idea will do

Gee! I don't really know.
Usually we work from objects that are nicely symmetrical in some way.

The rod should have a surface distribution that would only depend on the angle. And the summation of the electric fields of all infinitesimal charges should come out as expected.
But that's not easy to work through.

 

[Infinitum]

It is not an easy problem. Putting a conducting body in an electric field, it redistributes the charge on the conductor, and the charge distribution on the body - either having a net charge or not - influences the field near itself. The external electric field produces such surface charge distribution that the surface of the conductor becomes equipotential. This also means that the lines of the resultant field are perpendicular to the surface. And the relation of the surface charge density σ and the resultant electric field E_r at a place is σ = ε₀E_r
And of course, the electric field inside the conductor is zero.

ehild

Gee! I don't really know.
Usually we work from objects that are nicely symmetrical in some way.

The rod should have a surface distribution that would only depend on the angle. And the summation of the electric fields of all infinitesimal charges should come out as expected.
But that's not easy to work through.

I was also thinking along similar lines. Assuming the field perpendicular to the surface of the rod, I believe it would vary linearly with the thickness of the rod... I have no mathematical proof for this, though...

 

[ehild]

I think it would be interesting to solve the simpler problem first: A plate of large area A and small thickness d, with Q excess charge, put into a homogeneous electric field E, perpendicular to the plate. What is the surface charge density on both sides of the plate?

ehild

 

[Saitama]

I think it would be interesting to solve the simpler problem first: A plate of large area A and small thickness d, with Q excess charge, put into a homogeneous electric field E, perpendicular to the plate. What is the surface charge density on both sides of the plate?

ehild

I am not sure about it but i guess we can solve it by the hints provided by ILS.

 

[I like Serena]

I am not sure about it but i guess we can solve it by the hints provided by ILS.

Since you're not sure, care to give it a try? ;)

 

[Saitama]

Since you're not sure, care to give it a try? ;)

Since we have kept it in a uniform field E, an equivalent but opposite in direction, a field gets induced in the plate. As ILS said, the field inside inside is equal to ΔQ/Aε_o, therefore ΔQ=AEε_o. I am not sure how this charge will appear on the surface, i mean i know the charge will go to outer surface but how will this affect the outer surface charge distribution, what will be the final charge on outer surface and what's the use of the small thickness "d" that ehild has provided?

 

[ehild]

Since we have kept it in a uniform field E, an equivalent but opposite in direction, a field gets induced in the plate. As ILS said, the field inside inside is equal to ΔQ/Aε_o, therefore ΔQ=AEε_o. I am not sure how this charge will appear on the surface, i mean i know the charge will go to outer surface but how will this affect the outer surface charge distribution, what will be the final charge on outer surface and what's the use of the small thickness "d" that ehild has provided?

That d is small means only that the extension of the plate can be considered very big - infinite- with respect to thickness. Otherwise you need to consider the "edge effects". The value of the thickness does not influence the result if it is very small with respect to the lateral sizes.

When the plate is placed in the electric field, the field appears inside the plate at the first instant. The electric field inside moves the free electrons of the conductor till they reach the surface. Also free electrons will flow from the opposite surface towards the inside of the conductor to make the inside neutral. We say that the applied electric field induces excess surface charge; positive on one side of the plate and negative on the other side. The resultant surface charges cause such an electric field that is opposite to the applied field and cancels it inside the plate.

You need to find the amount of surface charge which appears on both sides of the plate when an electric field E is applied.

When the conductor has a net charge Q, it will change the outer field. Find out the resultant field on both sides of the plate.

ehild

 

[Infinitum]

Assume the electric field outside also enters the conductor. This would have a field E to the right(inside the conductor), going by your diagram. Now the conductor plate needs a field E to the left, to counterbalance the external field, and hence redistributes charge. Taking a charge Q₁ for one side of the plate, equate the field sum to E.

 

[Saitama]

The initial charge on both the surfaces were Q/2, when we place the plate in electric field, the final charge will be Q/2-AEε_o and Q/2+AEε_o, am i right?

 

[I like Serena]

Close! :)

What is your resulting ΔQ between the charge on the left and the charge on the right?

 

[Saitama]

Close! :)

What is your resulting ΔQ between the charge on the left and the charge on the right?

2AEε_o?

 

[ehild]

The initial charge on both the surfaces were Q/2, when we place the plate in electric field, the final charge will be Q/2-AEε_o and Q/2+AEε_o, am i right?

It is correct.

ehild

 

[Saitama]

It is correct.

ehild

Ah, thanks ehild! But i am still confused on which surface, Q/2-AEε_o or Q/2+AEε_o will reside? Any clarification on that will help.

 

[ehild]

Ah, thanks ehild! But i am still confused on which surface, Q/2-AEε_o or Q/2+AEε_o will reside? Any clarification on that will help.

The charge will reside on both surfaces of the plate. If the applied electric field points to the right, Q/2+AEε₀ charge is on the right-hand side surface of the plate and Q/2-AEε_o is on the left-hand side.

ehild

 

[Saitama]

The charge will reside on both surfaces of the plate. If the applied electric field points to the right, Q/2+AEε₀ charge is on the right-hand side surface of the plate and Q/2-AEε_o is on the left-hand side.

ehild

Thank you ehild! I get it now.