Charge transfer between two capacitors in an open circuit

[juvan]

Hello everyone,

I have drawn a picture of my confusion, I think it says it all:

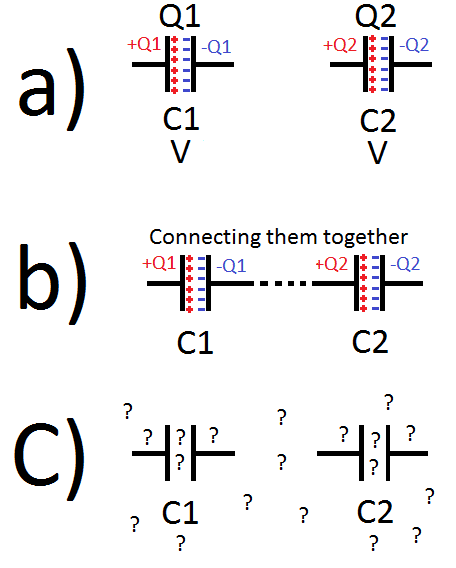
Now to add some text: so we charge two capacitors C1 and C2 to a voltage V. Now we have two charged capacitors. We now connect -Q1 to +Q2 and nothing else (the other two legs are floating). From my basic understanding of physics opposite charges attract so in our case I feel as though there should be some charge movement, even though we don't have a closed circuit (basic electronics) we still have opposite charges connected by a conductor (basic physics).

I am asking for an overall explanation of the scenario. What I would like most is not an explanation with equations but with simple words and the physical goings on.

Thank you.

 

[Philip Wood]

As I suspect you know, nothing much happens when your dotted line in (b) is made a conductor. Here are two remarks which might help.

(a) The charges on the 'inner' plates (B and C, to steal Qwertywerty's notation) are locked in place by the attraction of the charges on the outer plates (A and D).

(b) Electric field lines start on positive charges and end on negative charges. Capacitors (certainly those for electronics) are so constructed that there's almost no chance of a field line starting on the positive plate ending anywhere except on the other plate: the charges on the plates are equal and opposite.

(d) Another approach. Take plates A and D away. Free electrons on B will move to C so there'll no longer be any charge separation; the B/C assembly will be neutral. Now gradually move charged plates A and D into place. The positive charge on A will draw some free electrons from C into B, and the negative charge on D will assist in pushing the free electrons in the same direction.

PS Lovely diagrams – how did you do them?

 

[Qwertywerty]

I am asking for an overall explanation of the scenario. What I would like most is not an explanation with equations but with simple words and the physical goings on.

First of , you should know that charges on the inner surfaces of the capacitor plates will be the same always .
Also , charges are not going to jump from one plate to another .

I'll assume that , from left to right , the plates are numbered A , B , C and D .
Now , obviously , when you connect two objects with different charges , there is a flow of the charges from the more charged particle to the lesser charged particle ( Potential difference ) . Same in this case from - B to C .
There will be a flow till charge on B is equal to that on C . Simultaneouly , charges on A and D will move towards their outer surface , such that net charge in between each capacitor's plates is zero .

Hope this helps ,
Qwertywerty .

 

[stedwards]

It helps to look at it the other way around. Charge the two capacitors in series then separate them. Nothing special happens.

You can even assign a potential of zero volts to the center node, if that helps.

 

[nasu]

First of , you should know that charges on the inner surfaces of the capacitor plates will be the same always .
Also , charges are not going to jump from one plate to another .

I'll assume that , from left to right , the plates are numbered A , B , C and D .
Now , obviously , when you connect two objects with different charges , there is a flow of the charges from the more charged particle to the lesser charged particle ( Potential difference ) . Same in this case from - B to C .
There will be a flow till charge on B is equal to that on C . Simultaneouly , charges on A and D will move towards their outer surface , such that net charge in between each capacitor's plates is zero .

Hope this helps ,
Qwertywerty .

This is not necessarily true. The charge will flow until (and if) there is a potential difference and will stop when they are the same potential (and not the same charge).
If we assume ideal capacitors, the field outside the plates is zero so there is no field between the capacitors and so, no potential difference. The charge has no "reason" to flow.
If we consider edge effects, there is a field, for sure. But then you cannot apply the simple capacitor formulas.

It's just an illusion that there is a net force moving charge from plate C to B (for example).
The positive charge on the plate C is attracted by the negative on D as well as the negative on B and also repelled by the positive on A. For ideal capacitor, the forces from A and B cancel out.

 

[juvan]

Ok... I think I get what you are all saying and thank you for the replies. All the answers combined really helped, the only slightly confusing answer was 'Qwertywertys'.

It helps to look at it the other way around. Charge the two capacitors in series then separate them. Nothing special happens.

This helped to support what 'Philip Wood' and 'nasu' said.

What I got from it is that the electric field in a capacitor is present (for the most part) only between the plates, so the charges on plate A are attracting charges on plate B (and the same for plates C and D). Now even if there are different charges on plates B and C and the charges are connected via conducting wire, the electric field is much stronger in the capacitors (A to B and C to D) then through the wire (B to C) and although there may be some tiny charge transfer, the charges mainly stay where they are. That seems intuitive, I obviously haven't thought about the electric field. Is my reasoning correct?

PS Lovely diagrams – how did you do them?

MS Paint :)

 

[Philip Wood]

MS Paint :)

Thank you.

It's easy to check the prediction about capacitor behaviour using real capacitors. The pd across a capacitor is proportional to the magnitude of the charge, so the prediction can be checked by looking for abrupt changes in p.d. across either capacitor when the connection is made.

There are practical considerations. A cheap autoranging digital multimeter usually has a resistance of about 10\ \textrm{M} \Omega on its volts range, so you'll need capacitors of a least several \mu \textrm{F} so that voltage doesn't decay too quickly by leakage through the meter.