vis viva
- 29
- 10
As I understand both cations and electrons are produced between cathode and anode in a gas discharge, but what is their imminent fate, during and post discharge event? The majority of information I could find only covers the electrons from the time of the first ionization event to impacting the anode, but no word about what happens afterwards, and the cations are not mentioned at all either.
For the purpose of education, let's assume open air discharge.
For reference, taken from wiki
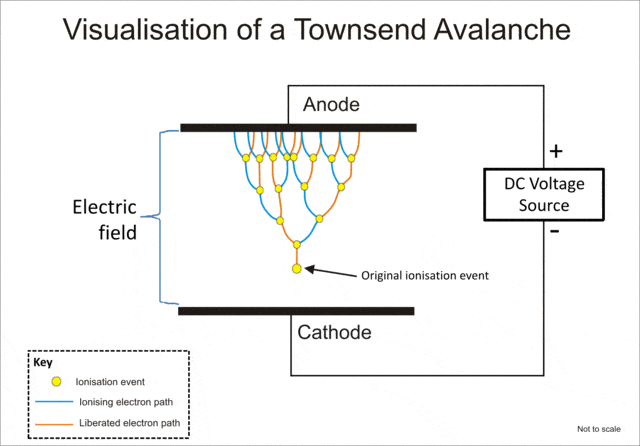
For the purpose of education, let's assume open air discharge.
For reference, taken from wiki