M. M. Fahad Joy
- 25
- 2
Member warned that the homework template must be used.
Known data:
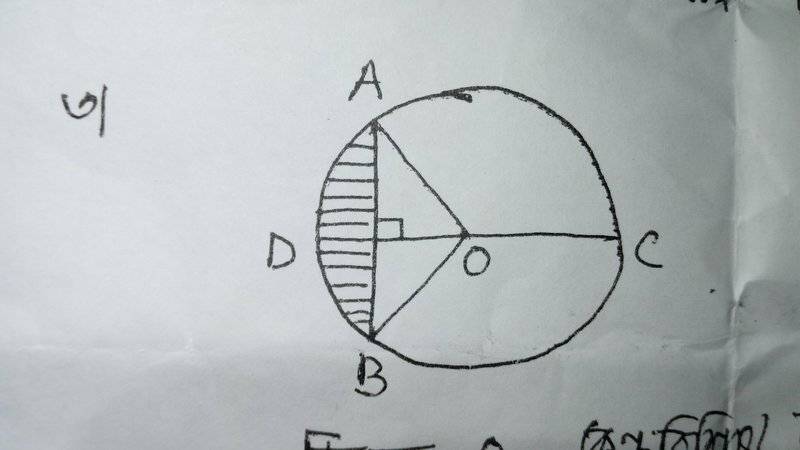
In the picture, CD = 10 cm. What is the area of shaded area?
Equation:
I know,
Area of a circle = ##πr^2##
Diameter of a circle = ##2πr##
Attempt:
Here, ## r = 10/2 = 5 ##
So, diameter ## = 2πr = 2*3.1416*5 = 31.42 cm ##
And area of the circle ## = πr^2 = 3.1416*5^2 = 78.54 cm^2 ##
But I don't know how to find out the area of sheded section.
Please help me.
In the picture, CD = 10 cm. What is the area of shaded area?
Equation:
I know,
Area of a circle = ##πr^2##
Diameter of a circle = ##2πr##
Attempt:
Here, ## r = 10/2 = 5 ##
So, diameter ## = 2πr = 2*3.1416*5 = 31.42 cm ##
And area of the circle ## = πr^2 = 3.1416*5^2 = 78.54 cm^2 ##
But I don't know how to find out the area of sheded section.
Please help me.
Attachments
Last edited:

