Mario
- 2
- 0
Hi,
i have this problem..., giving two circle (example radius 1 = 500 units, radius 2 = 200 units, distance between centers = 275.73 units) find Euler Spiral (aka Cornu spiral, aka Clothoid https://en.wikipedia.org/wiki/Euler_spiral) tangent giving circle (unknown tangent points).
For this problem are two mirrored Euler spiral as solution with length = 450 units.
Problem so simply to explain but not so simply to find solution...
Many thanks for help...
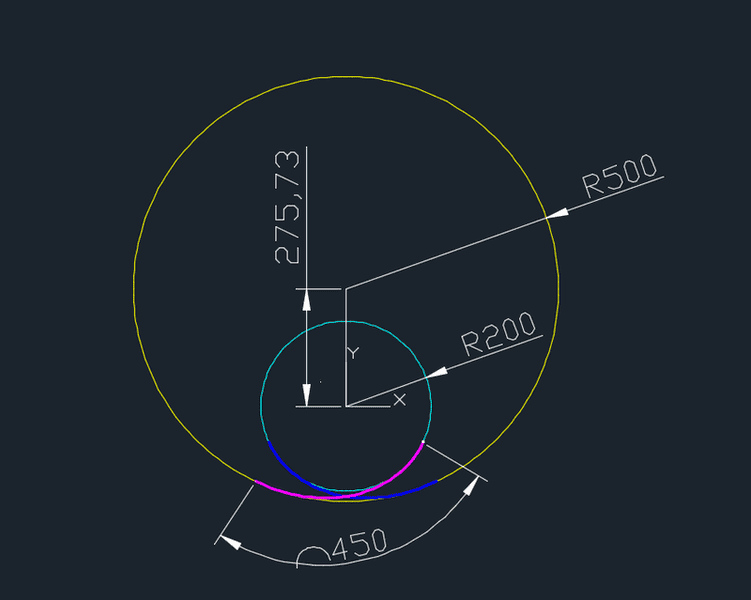
i have this problem..., giving two circle (example radius 1 = 500 units, radius 2 = 200 units, distance between centers = 275.73 units) find Euler Spiral (aka Cornu spiral, aka Clothoid https://en.wikipedia.org/wiki/Euler_spiral) tangent giving circle (unknown tangent points).
For this problem are two mirrored Euler spiral as solution with length = 450 units.
Problem so simply to explain but not so simply to find solution...
Many thanks for help...
 again, too
again, too