- #1
hastings
- 80
- 0
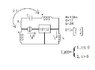
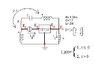
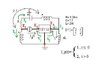
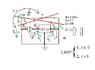
Given the following circuit: (see attached file)
find the Network Function between I_L, flowing as drawn in picture, AND I_g.
I guess all the calculation should lead up to an expression like this one:
I_L(s)=F(s) I_g(s), where F(s) is a function in "s" which corresponds to the NETWORK FUNCTION we're looking for.
This means we have to work in Laplace's domain.
I know I have to "translate" the circuit elements into Laplace's domain so that all the resistors, capacitors and inductors contain Laplace's complex variable, "s".
R --> R
C --> 1/(sC)
L --> sL
"Y" network --> 1) I_1= 2V_1 -V_2 ; 2) I_2= -V_1 +2V_2
I_1, I_2 are the currents flowing into the network while V_1, V_2 are the Voltage drops between the lateral points and the central point/junction.
Ideal transformer (remember n=2 ?) ---> 1) I_3 = 2 * I_4 ; 2) V_3 = -1/2 * V_4
I_3, V_3 are the current and voltage of the vertical inductor linked by the arrow in the picture, to the horizontal one in the upper part of the picture, I_4 and V_4.
Also, I_1 = I_g and should be substituted in the 1st equation of the the "Y" network.
Now, how do I proceed?
find the Network Function between I_L, flowing as drawn in picture, AND I_g.
I guess all the calculation should lead up to an expression like this one:
I_L(s)=F(s) I_g(s), where F(s) is a function in "s" which corresponds to the NETWORK FUNCTION we're looking for.
This means we have to work in Laplace's domain.
I know I have to "translate" the circuit elements into Laplace's domain so that all the resistors, capacitors and inductors contain Laplace's complex variable, "s".
R --> R
C --> 1/(sC)
L --> sL
"Y" network --> 1) I_1= 2V_1 -V_2 ; 2) I_2= -V_1 +2V_2
I_1, I_2 are the currents flowing into the network while V_1, V_2 are the Voltage drops between the lateral points and the central point/junction.
Ideal transformer (remember n=2 ?) ---> 1) I_3 = 2 * I_4 ; 2) V_3 = -1/2 * V_4
I_3, V_3 are the current and voltage of the vertical inductor linked by the arrow in the picture, to the horizontal one in the upper part of the picture, I_4 and V_4.
Also, I_1 = I_g and should be substituted in the 1st equation of the the "Y" network.
Now, how do I proceed?