Circular Motion/Energy: Find the position of the rings when tension = 0

[Edidas]

Homework Statement

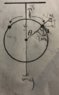
A smooth circular track of mass m is vertically hung by a string down the ceiling. Two small rings, each of mass 3m are initially at rest at the top of the track. They then slide down simultaneously along the track in opposite directions. Find the position of the rings when the tension in the string is zero.

Relevant Equations

Conservation of Energy
mgh = 1/2mv^2
Centripetal Force
Fc = mv^2/r

Here's my first attempt at a solution:

First, I calculated the speed of one ring at the point where the tension would be zero.
3mgr(1-cosΘ ) = (1/2) * (3m) * (v^2).
3m * v^2 = 6mgr(1-cosΘ)

Next, since I wanted the centripetal force, I took the result I got and divided by the radius.
Fc = 6mg(1-cosΘ)

Since I wanted to balance the forces, I calculated the normal force of the hoop on one of the rings.
N - (3mg * cosΘ) = Fc
N = 3mg * (2 - cosΘ)

Then to balance the vertical, I needed the vertical component of the normal force to be equal to the weight of the large hoop. Since there were two rings, I multiplied my initial result by 2.
2 * N * cosΘ = mg.

Simplifying, I got:
6 cos^2(Θ) - 12 cos (Θ) + 1 = 0

The correct answer was Θ = 73° and I do not understand where my error is. I do suspect that it may be in my normal force calculation or the balancing of the vertical forces.

Thanks.

 

[haruspex]

N - (3mg * cosΘ) = Fc

Check that by considering special cases of the angle.

 

[kuruman]

First, I calculated the speed of one ring at the point where the tension would be zero.
3mgr(1-cosΘ ) = (1/2) * (3m) * (v^2).
3m * v^2 = 6mgr(1-cosΘ)

Why does this equation give the point where the tension is zero? It looks like the mechanical energy conservation equation that applies to all points.

 

[haruspex]

Why does this equation give the point where the tension is zero? It looks like the mechanical energy conservation equation that applies to all points.

That bothered me until I realized @Edidas had mentally defined the angle theta to be that point. Of course , the equation is true for all theta.

 

[Edidas]

Check that by considering special cases of the angle.

I looked at when Θ = 0° and determined that N = 3mg so in that case would it be N + 3mgcosΘ = Fc?

 

[kuruman]

That bothered me until I realized @Edidas had mentally defined the angle theta to be that point. Of course , the equation is true for all theta.

So $\theta$ and $v$ are their respective "critical" values such that the tension is zero. This is appears backwards to me, but OK.