Circular Motion: What is the Radius of Curvature Near Maximum Height?

[vipulgoyal]

Homework Statement

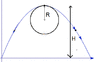
a stone is projected at an angle with the horizontal with velocity u. it executes a nearly circular motion near its maximum height for a short time. the radius of circular path is
??`

Homework Equations

answer is u² sin²x/g3. The Attempt at a Solution
why isn't it is just the maximum height?

 

[cupid.callin]

why isn't it is just the maximum height?

I can't understand what you are asking

 

[vipulgoyal]

I can't understand what you are asking

i just want to know the radius of the circular path exhibited by the stone at the top of its path

""why it isn't the maximim height"" i mean that answer should be the mximum height attained by the body

 

[cupid.callin]

no it won't be max height

like in this case:

H is max height but radius is R

 

[vipulgoyal]

no it won't be max height

like in this case:

H is max height but radius is R

yeah... thnx

but still don't know how to find R ??

 

[cupid.callin]

(Its late now ... must sleep or take steroids :zzz:)

use the eqn:

$$a_{radial} = \frac{v^2}{Radius}$$

and here v will be tangential to the curve obviously

(off to sleep :zzz:)

 

[vipulgoyal]

thnx man.. jus got it right

 

[tiny-tim]

hi vipulgoyal!

it is asking you for the radius of curvature at the top

hint: what is the speed at the top? ​