- #1
Carbon123
- 55
- 1
Homework Statement
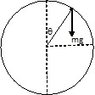
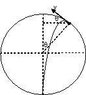
A ball was placed in a frictionless circular track with radius R and given initial velocity of u.The ball went around the cricle ,left at some point,then arrived in the same initial position after undergoing projectile motion.
a.State the speed u in terms of R and g
b.Coordinate of the ball when it left the circle.
Homework Equations
Conservation of energy
F=mv^2/R
The Attempt at a Solution
I assumed that the ball left at angle theta with the horizontal from the circle.therefore ,its height is R(1+sin(x)) then the ball takes off,the normal force is 0.Therefore speed at takeoff is v = gRsin(x).Using conservation of energy i was able to get u=gR(2+3sin(x)
From this point on I am kind of stuck to find the angle x ,and I do not know how to solve it.I tried to analyze the projectile motion,but i am still stuck.Help please ?
Thanks in advance