Circular ring and potential at its centre.

AI Thread Summary
To find the electric potential at a point on the axis of a uniformly charged circular ring, the charge on a small length of the ring can be treated as a point charge. The potential due to this charge is calculated using the formula V = Kq/r, where K is the Coulomb's constant, q is the charge, and r is the distance from the charge to the point of interest. The total potential is obtained by integrating the contributions from all segments of the ring. Additionally, the electric field at that point can be derived as the spatial derivative of the voltage. Understanding these calculations is essential for solving problems involving charged rings.
lavanyasharma
Messages
1
Reaction score
0

Homework Statement


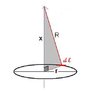
Consider a circular ring of radius r, uniformly hcarged with linear density lambda. Find the electric potential at a point on the axis at a distance x from the centre of the ring. Using this expression for the potential, find the electric field at this point.


Homework Equations



V = Kq/r
Electric field = spatial derivative of voltage

The Attempt at a Solution


I'm having trouble finding the potential! I do not understand how to calculate the potential due to a ring? I can't assume it to be a point hcarge!
 
Physics news on Phys.org
lavanyasharma said:
I'm having trouble finding the potential! I do not understand how to calculate the potential due to a ring? I can't assume it to be a point hcarge!

The charge carried on a small length dl can be considered as point charge. Calculate the contribution of the charge dq=Lambda*dl to the potential at x and integrate round the ring.

ehild
 

Attachments

  • chargering.JPG
    chargering.JPG
    7.6 KB · Views: 520

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

How Is the Electric Field Calculated for a Point Outside a Charged Ring?
Replies
11
Views
3K
What's wrong? Electric potential of a point on a ring
Replies
10
Views
2K
Total Potential of a Ring at Point P
Replies
13
Views
1K
Prove that the field due to a circular arc is same as its bounded tangent at the centre of curvature
Replies
23
Views
982
Why is electric field at the center of a charged disk not zero?
Replies
4
Views
3K
Why is a current ring approx a magnetic dipole from very far off?
Replies
7
Views
2K
Potential V at point P on the axis of the ring.
Replies
1
Views
1K
Calculating Electric Potential for a Non-Negligible Thickness Toroid
Replies
4
Views
2K
Doubts about the electric field created by a ring
Replies
6
Views
2K
Force between charged Ring and Rod, disproved Newtons 3rd law?
Replies
3
Views
2K

Hot Threads

Recent Insights

Back
Top