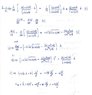Alexanddros81
- 177
- 4
Homework Statement
13.34 The curved portion of the cloverleaf highway interchange is defined by
##R^2=b^2sin2θ##, 0<=θ<=90deg. If a car travels along the curve at the constant speed v0,
determine its acceleration at A
Homework Equations
The Attempt at a Solution
[/B]
Is this wrong?