- #1
KarenRei
- 100
- 6
Hi all. I've been working on this for two days and I feel embarrassed that I haven't been able to figure it out. I'm dealing with the following cocurrent diffusion situation between an aqueous and gaseous flow moving at the same velocity:
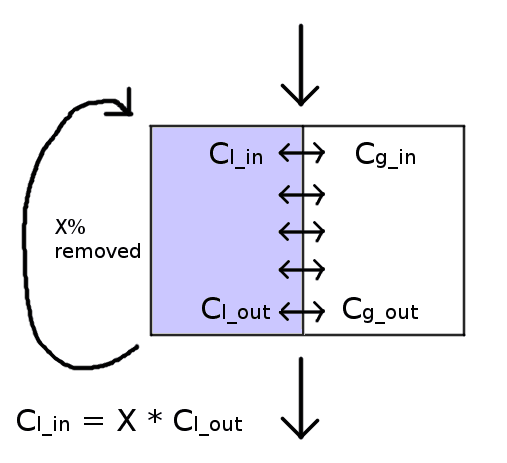
X% of the liquid is removed and replaced with fresh (0% concentration) each runthrough, so the incoming liquid concentration C_l_in is X% of the outgoing liquid concentration C_l_out. The incoming gas concentration C_g_in is known. The diffusion constant and Henry's law constants are also known, as is the length of time the two are in contact, the total contact area, and the flow rates of both the liquid and gas phases
It seems this should be a common use case, but while I find tons of articles on Fick's Law and diffusion, all of my wading through them hasn't revealed any covering this case. And I've been trying to derive it on my own, but I suck at differential equations. :( Does anyone know how to solve for C_l_out and C_g_out?
(In case it matters: the above diagram is stylized; in practice it's droplets entrained in a gas stream)
X% of the liquid is removed and replaced with fresh (0% concentration) each runthrough, so the incoming liquid concentration C_l_in is X% of the outgoing liquid concentration C_l_out. The incoming gas concentration C_g_in is known. The diffusion constant and Henry's law constants are also known, as is the length of time the two are in contact, the total contact area, and the flow rates of both the liquid and gas phases
It seems this should be a common use case, but while I find tons of articles on Fick's Law and diffusion, all of my wading through them hasn't revealed any covering this case. And I've been trying to derive it on my own, but I suck at differential equations. :( Does anyone know how to solve for C_l_out and C_g_out?
(In case it matters: the above diagram is stylized; in practice it's droplets entrained in a gas stream)