Coefficient of restitution in different frames of references

[Roman.G]

To simplify my question I would like to use a random example (although, the issue holds regardless of the numbers you pick). Suppose two objects collide (head-on) in one dimension. The initial parameters are as follows (units are irrelevant):

m1=1;m2=2;u1=3;u2=-4;

Also, suppose that exactly 90% of the KE is lost as a result of the collision (hence, the coefficient of restitution is sqrt(0.9)). Now I can convert both velocities into the center-of-mass frame of reference, invert them, multiply by sqrt(0.9) and convert back into the lab frame of reference to get (one of the two solutions):

v1=-6.09384 and v2=-0.54692

The problem with these numbers is: if I keep everything in the lab frame of reference and plug all these numbers into these equations (where ε=0.9):

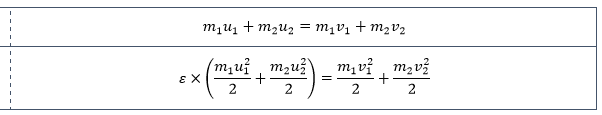
their LHS is not equal to their RHS by quite a significant quantity.

What am I missing?

Thanks!

 

[jbriggs444]

their LHS is not equal to their RHS by quite a significant quantity.

What am I missing?

If the objects have a non-zero total momentum in the lab frame then the system as a whole will have residual kinetic energy based on total mass and velocity of the center of mass, even when the component objects have all come to rest with respect to each other. As long as mass and momentum are conserved, this kinetic energy cannot go away. The coefficient of restitution can be thought of as the fraction of kinetic energy retained during each collision above and beyond that residual amount which is always retained.

If you included that residual energy when multiplying by 0.9 then your calculations would result in an energy deficit of 0.1 times residual energy, compared with reality.