seel
- 4
- 0
- TL;DR Summary
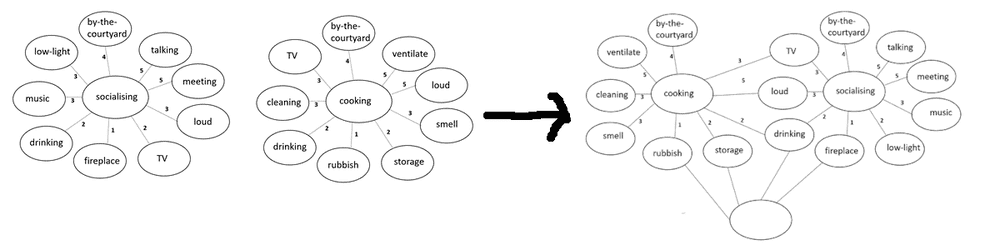
- We are trying to find a way to combine individual graphs into one.
We are working on an architectural project using graphs and we are looking for a way to combine separate graphs into one. We looked into methods to generate graph homorphisms, following the maximum graph homomorphism (MGH) (Langberg et al. 2006) and Paweł Rzążewski’s Exact Algorithm (2014), which maps adjacent vertices in separate graphs. We are using an undirected weighted graph (as we need to establish weights of the links bt nodes). Any help with this project would be great!