ifihadsomebacon
- 4
- 0
Going from:
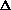 E = q + w
E = q + w
To:
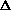 H =
H =
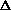 E +
E +
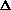 (PV)
(PV)
I'm confused as to why you add the product of the pressure and volume of the system to the internal energy to get enthalpy. Is it just because "that's what enthalpy is defined as"? I think I understand that when holding pressure constant, the
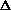 (PV) becomes P
(PV) becomes P
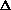 V and cancels with the w = P
V and cancels with the w = P
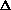 V from
V from
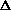 E, giving
E, giving
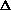 H = q. If pressure is not constant, does that mean
H = q. If pressure is not constant, does that mean
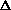 H = q + w +
H = q + w +
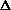 (PV) or
(PV) or
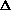 H = q + P
H = q + P
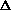 V +
V +
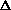 (PV) is true? What does this mean, practically? I just am wondering why are there two "PV" expressions in the first place? What even is
(PV) is true? What does this mean, practically? I just am wondering why are there two "PV" expressions in the first place? What even is
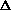 (PV)? It doesn't make sense to me like P
(PV)? It doesn't make sense to me like P
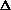 V, what about
V, what about
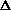 (PV) makes it so it can be added on initially?
(PV) makes it so it can be added on initially?
I know I asked a lot of questions, I'm just trying to make my confusion clear. (Ha)
To:
I'm confused as to why you add the product of the pressure and volume of the system to the internal energy to get enthalpy. Is it just because "that's what enthalpy is defined as"? I think I understand that when holding pressure constant, the
I know I asked a lot of questions, I'm just trying to make my confusion clear. (Ha)
Attachments
-
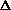 delta.gif63 bytes · Views: 2,944
delta.gif63 bytes · Views: 2,944 -
 delta.gif63 bytes · Views: 3,109
delta.gif63 bytes · Views: 3,109 -
 delta.gif63 bytes · Views: 2,925
delta.gif63 bytes · Views: 2,925 -
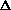 delta.gif63 bytes · Views: 3,025
delta.gif63 bytes · Views: 3,025 -
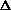 delta.gif63 bytes · Views: 2,864
delta.gif63 bytes · Views: 2,864 -
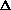 delta.gif63 bytes · Views: 2,734
delta.gif63 bytes · Views: 2,734 -
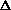 delta.gif63 bytes · Views: 2,631
delta.gif63 bytes · Views: 2,631 -
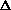 delta.gif63 bytes · Views: 2,714
delta.gif63 bytes · Views: 2,714 -
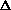 delta.gif63 bytes · Views: 2,726
delta.gif63 bytes · Views: 2,726 -
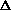 delta.gif63 bytes · Views: 2,714
delta.gif63 bytes · Views: 2,714 -
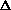 delta.gif63 bytes · Views: 2,754
delta.gif63 bytes · Views: 2,754 -
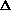 delta.gif63 bytes · Views: 2,588
delta.gif63 bytes · Views: 2,588 -
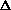 delta.gif63 bytes · Views: 2,748
delta.gif63 bytes · Views: 2,748 -
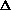 delta.gif63 bytes · Views: 2,702
delta.gif63 bytes · Views: 2,702 -
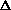 delta.gif63 bytes · Views: 2,613
delta.gif63 bytes · Views: 2,613 -
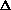 delta.gif63 bytes · Views: 2,735
delta.gif63 bytes · Views: 2,735 -
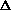 delta.gif63 bytes · Views: 2,764
delta.gif63 bytes · Views: 2,764