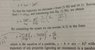Craig Scott
- 10
- 2
Homework Statement
1. How did they complete the square for these equations in the picture below? What was their thought process?
2. distance/velocity = time , velocity/acceleration = time , In leibniz notation how does this cancel out?
When you divide, how does it cancel out to give you a time unit?
Homework Equations
1. In picture
2. ds/dt / d2s / dt2
The Attempt at a Solution
1. It seems like it came out of thin air.
2. dt/ds = time?