Complex number method for kinematic equations

[anonymous4l]

Homework Statement

Objective:
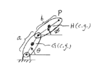
1. For a two-arm manipulator, use complex-number method to derive the displacement, velocity and acceleration equations for the tracing point P.
2. For a two-arm manipulator, use complex-number method to derive the displacement, velocity and acceleration equations for the center of gravity for each arm assuming it is located halfway between the joints.
3. Construction graphical solutions for 3 positions.

Homework Equations

The arm lengths are 1" each. angular velocity: ω=1rad/s, angular acceleration: α=1rad/s^2

The Attempt at a Solution

I get a little lost in the algebra.
So far I have a*e^(i*theta) + b*e^(i*phi) = x + i*y

I separated into real and imaginary:

Real: a*cos(theta)+b*cos(theta)=x

After dividing by i...I get:

Imaginary: a*(sin(phi)) +b*sin(phi) = y

Then I'm not sure what to do.

Thanks,

-D

p.s. If anyone knows how to model this in either MATLAB or excel...please email me!

 

[BruceW]

It's not quite right. for the real part, you've written theta in both cosines, but that's not right, if you think of the trigonometric form of a complex number. (And you've got a similar mistake for the imaginary part). Maybe write out the complex numbers explicitly in trigonometric form, instead of skipping this step.