ur5pointos2sl
- 95
- 0
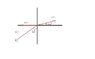
Use the component method to find the resultant(direction and magnitude) of the three forces shown.
Could someone please verify my answers or tell me where I went wrong.
Ax = 500 Cos 30 = -433N
Ay = 500 Sin 30 = -250N
Bx=-250 N
By= 0
Cx=200 Cos 20 = 187.9N
Cy= 200 Sin 20 = 68.4N
R = (-433-250+187.9)I + (-250 + 0 + 68.4)j
= (-495.1, -181.6)
R = sqrt(-495.1^2 + -181.6^2)
= 527N
Tan Theta = 318.4 / 370.9
Theta = 20.1 deg.
Could someone please verify my answers or tell me where I went wrong.
Ax = 500 Cos 30 = -433N
Ay = 500 Sin 30 = -250N
Bx=-250 N
By= 0
Cx=200 Cos 20 = 187.9N
Cy= 200 Sin 20 = 68.4N
R = (-433-250+187.9)I + (-250 + 0 + 68.4)j
= (-495.1, -181.6)
R = sqrt(-495.1^2 + -181.6^2)
= 527N
Tan Theta = 318.4 / 370.9
Theta = 20.1 deg.