- #1
Stealth849
- 38
- 0
Homework Statement
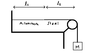
An aluminum wire of length l1 = 60cm, cross section area 1.00 x 10-2cm2, and density 2.60g/cm3, is joined to a steel wire of density 7.8g/cm3 and same cross sectional area. The compound wire loaded with a block of mass m = 10kg is arranged as shown so that the distance l2from the joint to the supporting pulley is 86.6cm. Transverse waves are set up in the wire using an external source of variable frequency. A node is located at the pulley.
a) find the lowest frequency of excitation for which a standing wave is observed to have a node at the joint.
b) How many nodes are observed at this frequency?
Homework Equations
f = v/λ = nv/2l
ρ = m/V
v = sqrt(FT/μ)
The Attempt at a Solution
Not too sure where to begin on this one. When it asks for the lowest frequency of excitation, I expect that means the second harmonic, because that would leave a node at the joint with the lowest frequency.
So knowing the densities of the wires, I can get v where
FT = μv2
FT = mg = 98N
μ = m/l = ρV/l = ρA where A represents the cross sectional area.
so μ1 = 2600*0.0001 = 0.26
μ2 = 7800*0.0001 = 0.78
v1 = sqrt(98/0.26) = 19.4m/s
v2 = sqrt(98/0.78) = 11.2m/s
so f = nv/2l
where n = 2 for the second harmonic
f1 = 2*0.26/(2*0.6) = 0.43Hz
f2 = 2*0.78/(2*0.866) = 0.90Hz
No idea if I'm approaching this correctly, due to the idea of reflection of waves at the joint.. Say a wave does reflect at the joint and a portion of it is sent back to the source, there would be a lot more waves thus being a much higher harmonic - not the second.
Any and all help appreciated. Thanks!
Attachments
Last edited: