- #1
Feodalherren
- 605
- 6
1. Homework Statement
CFD
I'm a bit confused by this question.
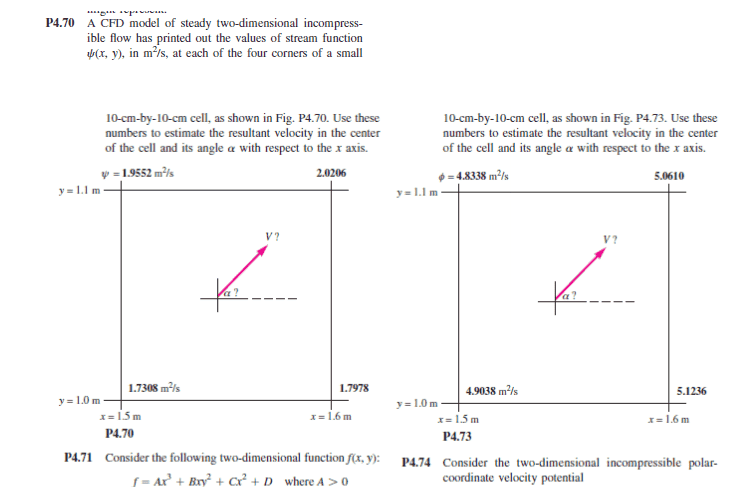
So at first what I do for the problem on the left, I find the changes in the velocities in X and and Y on all four sides.
I notice that the values on the diagram to the left are higher on top than they are on the bottom, therefore I conclude that v must be "up".
I also notice that the values are higher on the right than they are on the left, therefore I conclude that u is to the right.
For the diagram on the right: I notice that bottom > top, therefore v is down.
Right > left, therefore u is to the right.Are these assumptions correct?
After that it's a fairly simple problem but this first step has me confused as to what I'm supposed to be doing.
Homework Equations
CFD
The Attempt at a Solution
I'm a bit confused by this question.
So at first what I do for the problem on the left, I find the changes in the velocities in X and and Y on all four sides.
I notice that the values on the diagram to the left are higher on top than they are on the bottom, therefore I conclude that v must be "up".
I also notice that the values are higher on the right than they are on the left, therefore I conclude that u is to the right.
For the diagram on the right: I notice that bottom > top, therefore v is down.
Right > left, therefore u is to the right.Are these assumptions correct?
After that it's a fairly simple problem but this first step has me confused as to what I'm supposed to be doing.