cascadeless
- 11
- 0
Homework Statement
A bacteria that normally divides every 20 minutes express gene X. The production rate of protein X is 5nM/min. The protein is stable and does not degrade.
- What is the concentration of X in the steady state?
- The same bacteria enter into a stress state at t=0 for 3 hours (before t=0 the level of protein X is
at the steady state you found in a). In this state of X increases to 20nM/min but the cell division time changes to 60 min. Calculate the dynamic level of protein X starting t=0. What is the steady state in this case? - At t=3 hours the bacteria gets a signal that cases the protein X to become unstable with half-life of 10 min. Calculate now the dynamic level of protein X and the steady state. How would the maximal level of X change if the bacteria got this signal after only 1 hour?
Homework Equations
$$\beta ... \text{production rate}$$
• Degradation/dilution rate in units of 1/time
$$x\alpha = \alpha_{dil} + \alpha_{deg}$$
• Change in concentration of Y
$$dY/dt = \beta - \alpha Y$$
• Steady state (solving for dY/dt=0)
$$Y_{ST} = \beta / \alpha$$
Further information on "An Introduction to Systems Biology" by Uri Alon.
The Attempt at a Solution
[/B]
For the first, I have to determine alpha and beta. Beta is obviously 5, and I thought alpha is 1/20, thus 0.05. I am not sure if this is true since the assignment states that the protein does not degrade. Forgive me, I am not that into biology. So the steady state should be 5/0.05 = 100.
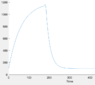
I am not sure how to do that with the time shift. I tried to plot it and see how it is looking, so I let MatLab solve the differential equation stated above with initial condition 100. When t is below 180 (3 hours) I set beta to 20 and alpha to 1/60. And when t is higher than 180 then I set the parameters as before. However, that looks like the following:
Unfortunately, I don't know how to calculate the dynamic level of protein X starting with t=0, that's the main problem which I also need for 3.
For 3 I've no idea currently.
I appreciate any help!