Computing Mass Distribution in Statics Problems

[Enrico Miccolis]

Hello,

I would like to ask the following question :

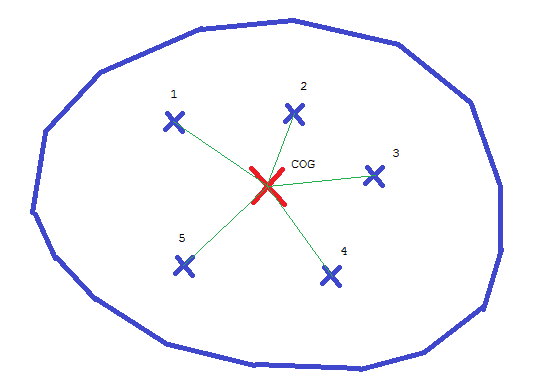
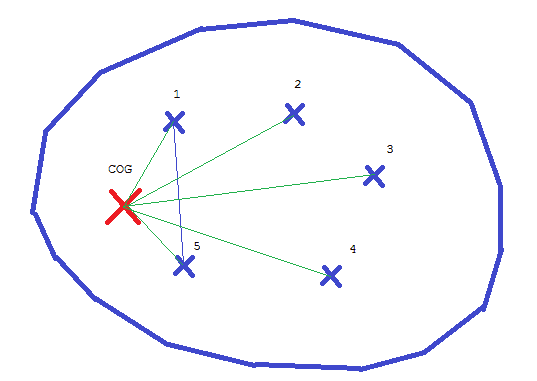
--> I have an object of mass M (represented by the blue potato in the two attached drawings).
--> I know the coordinates (x,y) of its Center of Gravity (reprensented by big red cross).
--> I also know the coordinates of its contact points to the ground (reprensented by the 5 bleue crosses).
(In this example, there are 5, but it can be more .. or less)

I would like to know how to compute the mass distribution amongst the various contact points.
(I assume that depending on where the COG lies in my Object... some contact points might act as a lever on the others and raise them from the ground).

Thanks in advance.
Enrico.

 

[Simon Bridge]

What you are describing is a statics problem - you should be able to think your way through it by comparing with the work you've probably done with a beam on supports.