Computing The Gravitational Force At A Point

[Bashyboy]

Homework Statement

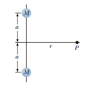
(a) Compute the vector gravitational field at a point P on the perpendicular bisector of the line joining two objects of equal mass separated by a distance 2a as shown in Figure P13.26. (b) Explain physically why the field should approach zero as r ---> 0. (c) Prove mathematically that the answer to part (a) behaves in this way. (d) Explain physically why the magnitude of the field should approach 2*(GM/r^2) as r --> infinity. (e) Prove mathematically that the answer to part (a) behaves correctly in this limit.

Homework Equations

The Attempt at a Solution

\vec{F}_0 = -2 \frac{Gmm_p}{\sqrt{r^2 + a^2}} \hat{i} is the equation I generated.

From the diagram, it is evident that, as r approaches zero, the point of interest becomes located in between the two fixed masses; furthermore, one can see that the two masses with pull equally in the j-hat direction, but anti-parallel, thereby causing all gravitational forces produced by the two masses to cancel. However, why is it that, when taking the limit as r --> 0, the mathematics does not show this?

 

[pasmith]

Your expression for the force is not dimensionally consistent, and so must be wrong. (You need GMm divided by a length squared; you have GMm divided by a length.)

It's usual to use M for the mass of fixed bodies and m for the mass of a test particle.

For each body, you need to determine the component in the \hat i direction of a force of magnitude GMm/(r^2 + a^2) directed along the line from (r,0) to the centre of the relevant body, and then add the two.

 

[Bashyboy]

Okay, I see that there shouldn't be a square root symbol in the denominator; however, I don't see what else is wrong with it. Both bodies pull equally in the -\hat{i} direction.

 

[gneill]

Okay, I see that there shouldn't be a square root symbol in the denominator; however, I don't see what else is wrong with it. Both bodies pull equally in the -\hat{i} direction.

Both bodies pull directly towards themselves. So, two force vectors, neither of which is directed along the -\hat{i} direction. What's the vector resultant?

 

[Bashyboy]

All right, let's see if I have properly determined the forces this time.

For one mass: \vec{F}_M = - \cos \theta \frac{GMm}{a^2 + r^2} \hat{i}, where \theta = arrcos(\frac{r}{\sqrt{r^2 + a^2}})

Is this correct?

 

[haruspex]

All right, let's see if I have properly determined the forces this time.

For one mass: \vec{F}_M = - \cos \theta \frac{GMm}{a^2 + r^2} \hat{i}, where \theta = arrcos(\frac{r}{\sqrt{r^2 + a^2}})

Is this correct?

Yes.