Conceptual question: translational and rotational equilibrium

[laica]

Homework Statement

There are two important conditions for a rigid body to be in equilibrium. The first condition is that the net force on a body must be zero. The second condition is that the net torque on a body must also be zero.


2,3. Relevant equations; attempt at solution.

I apologize for the simple question but I am self-studying physics and having a hard time with this concept.

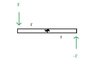
So my question is: how are these two conditions not redundant? My initial reaction is that net torque must be zero if net force is zero, since \tau=Fr. Then I drew this situation (a door revolving around a central pivot point) that seems to show net torque without net force (the 2 forces add up to zero but there is still rotation). The img is attached to this post.

The problem is, I still think net torque would be zero.
\tau=Fr
\tau=-Fr
\Sigma\\tau=(Fr)+(-Fr)=0

Where am I going wrong here? Is one radius -r maybe?

Thanks in advance!

 

[ehild]

The torque is the vector product of the radius-vector and the force. You have to handle both F and r as vectors.

Just thinking logically, the force on the left will rotate the rod anti-clockwise, and so will the force on the right. So the torques add, while the forces cancel.

ehild

 

[RoyalCat]

You've got your directions wrong. Torque is a vector quantity. That means that when you add two or more torques together to find the net torque, you must do so with due regard to sign.

The simplest way to add torques correctly, would be to use your intuition to find the "sense" of rotation of every force vector. For instance, in your example above, the left force tries to spin the rod counter-clockwise, while the right force tries to spin it counter-clockwise as well. Therefore, the net torque is the sum of the two, since the two torques have the same sense of rotation.
Were they opposite, then the direction of rotation would be determined by which is the greater torque.A more complete approach that you'll need for further studies, when keeping track of signs is a bit more important:
How do we take care of that sign, then? We define torque as a vector perpendicular to the plane of rotation (The plane of the lever arm vector and the force vector).

And we determine the sign by way of the right-hand rule (Wiki link:http://en.wikipedia.org/wiki/Right_hand_rule)

Torque as a vector is defined as:
\vec \tau = \vec r \times \vec F

Applying it to the situation above, taking the torque about the axis through the center of the rod, taking the positive direction as the one coming out of the plane of the page (If this is Greek to you, read up on the article on the right hand rule and vector cross product), we see a positive torque whose magnitude is 2Fr.