Confused by radial vs. centripetal acceleration

[eventob]

Hi

I've been working through some examples from the course material we use in physics class, but one thing keeps confusing me: What is the difference between centripetal and radial acceleration?

For instance, when we have a particle traveling in a circular path, the acceleration towards the center of the circle may be written as Ar (a sub r)=-Ac= - v^2/r, while other times it is written simply as Ac=v^2/r. The textbook (JS Physics for Scientists and Engineers) seems to use both.

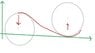
Where is the negative sign coming from? I made a quick sketch. Am I right if i think that the radial acceleration is negative in the first circle (to the left) and it is positive in the circle to the right? Is it just due to how I pick the axis and how I define positive direction?


Thanks in advance.

 

[Doc Al]

but one thing keeps confusing me: What is the difference between centripetal and radial acceleration?

Same thing.

For instance, when we have a particle traveling in a circular path, the acceleration towards the center of the circle may be written as Ar (a sub r)=-Ac= - v^2/r, while other times it is written simply as Ac=v^2/r. The textbook (JS Physics for Scientists and Engineers) seems to use both.

v^2/r is the magnitude of the radial acceleration; the direction is toward the center. Whether that's positive or negative just depends on how you define your sign convention.

Where is the negative sign coming from? I made a quick sketch. Am I right if i think that the radial acceleration is negative in the first circle (to the left) and it is positive in the circle to the right? Is it just due to how I pick the axis and how I define positive direction?

Yes.

 

[eventob]

Thank you very much. :)

 

[K^2]

Radial acceleration is equal to centripetal acceleration when the radius remains constant (with a +/- sign depending on definition). If radius changes as a function of time, you have to add the explicit second derivative of radius with respect to time.

a_r = a_c + \ddot{r} = -\omega^2 r + \frac{d^2r}{dt^2}

Similarly, tangential acceleration will pick up a term that depends on the second derivative of angle with respect to time and a Coriolis Effect term.